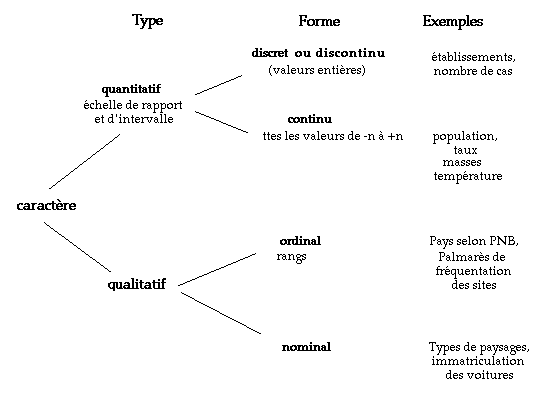
Selon le problème considéré différentes catégories de mesures peuvent être réalisées (cf.supra). Il est donc nécessaire de préciser la typologie des données esquissée ci-dessus. Selon la nature (propriétés) de ces données, différentes opérations seront possibles ou non. Il en découlera également la possibilité de les soumettre (ou non) à certains tests statistiques.
Ils relèvent des activités de mesure sensu stricto. Chaque cas individuel est mesuré en fonction d’une unité de mesure appropriée : les longueurs en m ou cm, les températures en ° C ou F, les nombres d’élèves en individus, etc. Chaque cas individuel fournit un résultat numérique qui correspond à un point sur une quelconque échelle de mesure standardisée (Standard Scalar Measurement).
Quand on compte le nombre d’élèves d’une classe, on mesure l’effectif sur l’échelle des nombres cardinaux. Dans ce cas, c’est une mesure absolue.
Dans tous les autres cas, on utilise une échelle de mesure relative qui donne une idée de l’importance de l’item mesuré.
Une même variable peut être mesurée avec différentes unités : les longueurs en m ou en yard, les prix en FF ou en Euros. Il est possible de les convertir de l’un à l’autre, lorsque l’on connaît la mesure d’une unité dans l’autre : 1 pouce (inch) = 2,54 cm ; 1 cm = 0,39 pouce (inch).
Cm et pouce, ou °C et °F sont des grandeurs commensurables. Par contre, cm et °C sont incommensurables.
En fonction des particularités des diverses unités, plusieurs échelles ont été définies pour caractériser les variables quantitatives.
Quand on mesure avec des cm, des pouces, des °C, l’intervalle entre 2 de ces unités reste toujours le même, quelle que soit la valeur.
Ceci est vrai aussi bien pour les mesures (m, kg, W, h, …, °C) que pour les dénombrements.
Cette propriété permet de réaliser des opérations arithmétiques et algébriques sur ces mesures :
5 cm + 3 cm = 8 cm ; 5 °C + 3 °C = 8 °C ; 12 étudiants — 4 étudiants = 8 étudiants.
Cette propriété va permettre de calculer certains paramètres comme la moyenne (cf. infra).
Les mesures réalisées en cm (longueur) ou en kg (masse), peuvent être subdivisées en autant de sous-multiples que nécessaire pour augmenter la précision de la mesure : 1,724 kg.
Les dénombrement d’étudiants ou de moutons sur une échelle cardinale ne peuvent donner lieu à fragmentation.
L’échelle continue s’oppose donc à l’échelle discrète ou discontinue.
L’échelle continue est infiniment divisible ; l’échelle discrète ou discontinue est composée d’éléments unitaires insécables.
Lorsque l’on mesure des longueurs (cm, inch) ou des effectifs (unités) on fait une mesure pour laquelle la valeur 0 = Zéro correspond à l’absence de longueur ou d‘effectif. C’est un zéro absolu, une quantité nulle.
Lorsque l’on mesure des températures en °C ou en °F, la valeur 0° ne correspond pas à une absence de température. Les conventions de mesure font qu’il peut y avoir des valeurs négatives.
Par contre, en °K (kevin), 0°K signifie absence de mouvement électronique, donc absence de température : 0°K = -273°C = -460°F
Les échelles de mesure qui présentent des intervalles égaux ET un 0 ZERO absolu sont des échelles de rapport : elles permettent de calculer des rapports : la longueur L est 3 fois plus grande que l.
Les autres sont des échelles d’intervalle, sans rapport possible : une température de 10°C n’est pas deux fois plus faible que 20°C.
Ces variables permettent de réaliser des sommes, des moyennes, des différences.
Sommes : la somme d’un ensemble de mesures à intervalles égaux ou sur une échelle cardinale est possible.
Moyennes : Les moyennes d’un ensemble de mesures sur échelle à intervalle égaux (rapport ou non) auront les propriétés de leur catégorie d’origine. L’exception est que les moyennes effectuées pour des valeurs discrètes accepteront des résultats continus, bien que l’unité de départ soit discrète : l’effectif moyen des groupes de TD est de 14,5 étudiants.
Différences : ici également les opérations sont possibles sur les différents types d’échelle quantitatives. Il sera possible d’appliquer le principe des rapports (A/B) non aux mesures elles-mêmes mais à leur différences : soit les valeur A = 40°C, B= 50°C et C=60°C ; on ne peut pas dire que B est 1,25 fois > que B, mais on peut dire sur la différence C-A est deux fois plus grande que B-A.
Toute situation où l’on peut dire qu’une valeur est inférieure < ou supérieure > à une autre permet de définir des relations d’ordre ou relations ordinales entre les éléments : 1er, 2ème, 3ème, …n nème.
Cela est vrai pour toutes les mesures faites sur une échelle d’intervalle égal (qui sont obligatoirement ordinales).
Dans certaines situations, comme l’absence d’appareil de mesure, on peut néanmoins estimer une mesure : dans nos régions, en hiver, la température intérieure est supérieure à la température extérieure. Point n’est besoin de thermomètre. On peut également définir des catégories ou classes de température : très chaud, chaud, froid, très frois, …
Par exemple, on demande de classer par ordre de préférence les objectifs orientant votre vie ; " bonne vie de famille — s’éclater avec des amis — plan de carrière d’enfer — gagner un tas de fric ". On attribuera le rang 1 à l’item le plus important, puis les rangs 2, 3, 4.
Bien que non quantitatif, le classement obtenu a un sens (comparer les scores 1-2-3-4 ET 4-3-2-1.
Cependant, rien ne prouve que les valeurs 1,2,3,4 correspondent à une graduation à intervalles égaux. En particulier, lorsqu’un même classement est choisi par plusieurs individus, rien ne prouve que cela ait le même sens.
Il ne sera donc généralement pas possible d’utiliser ces infos dans des opérations arithmétiques. La seule action possible est la mise en ordre, le classement.
On reprend le même problème que ci-dessus : classer les items Famille — Amis — Carrière — Argent.
Cette fois on attribuera à chaque catégorie une échelle les classant de 0 à 4 avec pour signification 0 = totalement futile, 1 = peu important, 2 = moyennement important, 3 = assez important et 4 = très important. Si, en plus, chaque valeur peut être graduée en décimales, nous obtiendrons par exemple :
Indiv A : F 4,0 ; A 3,8 ; C 3,6 ; M 3,4
Indiv B : F 4,0 ; A 3,5 ; C 2,0; M 1,0
Ce chiffrage permet de classer les catégories les unes par rapport aux autres. En plus, il sera possible d’avoir une indication de l’importance relative de chaque catégorie.
L’échelle de niveau apporte une information supplémentaire à l’échelle de classement. Cependant, rien ne prouve que chaque individu accorde la même importance aux valeurs de l’échelle.
Exemple : échelle de notation littérale ou chiffrée.
Egalement appelé mesure par catégorie.
Ce type de mesure implique que chaque item d’un ensemble d’items soit examiné pour définir si ses caractéristiques correspondent à l’une ou l’autre des catégories considérées.
Exemple : chez l’homme, la mesure du genre accepte 2 valeurs M ou F.
Il s’agit de catégories nominales pour lesquelles il n’y a pas d’échelle.
Dans d’autres cas, les catégories peuvent être ordonnées :
Exemple, parmi les grades universitaires : Bachelier, Licencié, Maître, Docteur.
Exemple, pour l’âge : jeune, mature, âgé.
Il s’agira de catégories ordinales.
Cela permet de calculer des fréquences et de constituer des tableaux de contingence.
Cela permet de considérer des ensembles d’individus différent par une seule variable (ex : sexe) (univarié) ou par deux variable (ex : sexe et âge) (bivarié) ou par plusieurs variables (sexe, âge, milieu) (multivarié).
Pour résumer : les données peuvent être divisées en deux grandes catégories :
Les données quantitatives, continues (dans l’échelle de rapport ou d’intervalle) ou discontinues,
Les données qualitatives, discontinues généralement, dans l’échelle ordinale (de rangement) ou dans l’échelle nominale.

Précision de la mesure (reliability)
Validité de la mesure (validity)
2. Echantillonner les dimensions de feuilles de deux espèces d’arbres
3. Exercices série 02