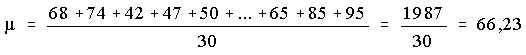
Les statistiques descriptives permettent de résumer l’information contenues dans un ensemble de données (population ou échantillon) par le calcul d’un ensemble de paramètres permettant d’en apprécier la variabilité. Il s’agit des paramètres de position, de dispersion et de forme de la distribution.
L’objectif théorique des statistiques descriptives est de fournir une caractérisation résumée de l’ensemble de données considéré, à travers le calcul des paramètres de position, dispersion et de distribution.
L’objectif pratique est de s’entraîner à l’usage correct de paramètres classiques comme moyenne, médiane, mode, écart type etc.
L’objectif concret est de maîtriser le calcul de ces paramètres en utilisant les moyens des feuilles de calcul ou ceux de l’informatique et de la télématique.
Les mesures de tendance centrale sont destinées à mesurer, au sens numérique du terme, « où » se situent les données le long d’un continuum donné. La notion de moyenne est apprise de bonne heure, de façon empirique, à travers les bilans trimestriels de notes obtenues par un élève, par exemple. Il peut également être apprécié par l’exemple suivant :
Pour subir une opération chirurgicale, un patient doit choisir entre les deux chirurgiens disponibles. Son appréciation est faite sur les résultats post-opératoires de la survie de leurs clients. Les données suivantes sont disponibles, 0 signifiant décès en cours d’opération :
Docteur A : 0, 0, 0, 0, 0, 0, 0, 0, 0, 55, soit m = 5,5
Docteur B : 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, soit m = 5
Honnêtement, est-ce que la connaissance de la moyenne est une information pertinente pour cette prise de décision.
Données groupées :
Il arrive que les données brutes ne soient plus disponibles parce que celles-ci ont déjà été regroupées en distribution de fréquences. Néanmoins, il demeure possible d'approximer les différentes mesures de synthèse
La moyenne ou valeur attendue (expected value, expectation) correspond à la moyenne arithmétique lorsqu’elle peut être numériquement calculée.
Méthode : c’est la somme des valeurs de tous les éléments (individus) constituant le jeu de données (échantillon), divisée par le nombre d’éléments de l’échantillon.
Exemple
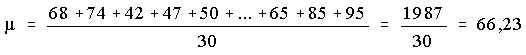
Si nous
considérons une population, la formule de la moyenne sera :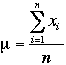 
Ici :
Si nous
considérons un échantillon, la moyenne sera :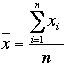 
Les deux formules sont identiques si ce n’est leur membre gauche.
Si nous considérons la moyenne ou valeur attendue (expectation) d’une population de données X, nous pouvons écrire : MU = E(X). E(X) se lit comme la valeur attendue (expectation) de X et est interprétée comme la moyenne arithmétique si elle peut être calculée.
Un des inconvénients de la moyenne empirique, vue comme valeur centrale d'un échantillon, est d'être sensible aux valeurs extrêmes. Une valeur manifestement très différente des autres est souvent qualifiée de valeur aberrante. Qu'elle soit ou non le résultat d'une erreur dans le recueil ou la transcription, on ne peut pas la considérer comme représentative.
Supposons que sur un échantillon de 10 valeurs, toutes soient de l'ordre de 10, sauf une, qui est de l'ordre de 1000. La moyenne empirique sera de l'ordre de 100, c'est-à-dire très éloignée de la plupart des valeurs de l'échantillon. Pour palier cet inconvénient, on peut décider ne pas tenir compte des valeurs extrêmes dans le calcul de la moyenne. On obtient alors une moyenne élaguée.
La formule est
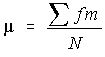
où :
Exemple
Résultat |
Nombre d'élèves (f) |
Centre de classes (m) |
fm |
| 40 et moins de 50 | 4 | 45 | 180 |
| 50 et moins de 60 | 6 | 55 | 330 |
| 60 et moins de 70 | 10 | 65 | 650 |
| 70 et moins de 80 | 4 | 75 | 300 |
| 80 et moins de 90 | 4 | 85 | 340 |
| 90 et moins de 100 | 2 | 95 | 190 |
| S | 30 | 1990 |
On calcule alors
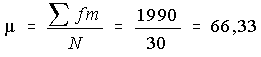
Ce qui est relativement proche de la «vraie» moyenne, c'est-à-dire µ = 66,23
Notes
On constate ici l'importance de
En effet, puisque la variable est discrète, le calcul effectué avec ces valeurs serait généralement plus précis, quoique, dans ce cas-ci, on obtiendrait µ = 65,83
Le mode correspond à la valeur la plus fréquemment observée dans un jeu de données (échantillon). Il peut y avoir plusieurs modes dans un échantillon, source de problèmes (homogénéité de la population ou de l’échantillonnage).
Exemples
Pour les données suivantes: 5, 6, 6, 7, 8, 8 il y a deux modes, soit 6 et 8
Pour les données du professeur Lecompte, la note la plus fréquente (3 fois) est 65
Le mode est aussi une mesure intéressante dans le cas qualitatif.
Reprendre l’exemple des docteurs A et B et déterminer le mode de chaque toubib.
Le mode peut être déterminé graphiquement comme la classe ayant la plus forte valeur en ordonnée (y).
Définition:
la classe modale est la classe qui a la plus haute
fréquence
Hypothèse: on suppose que le mode appartient à la classe modale
La formule est
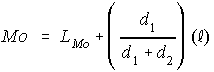
où
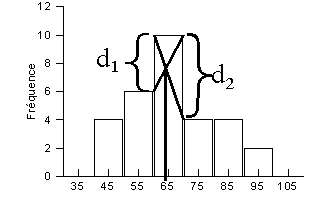
Exemple
La classe modale est «60 et moins de 70»
On calcule donc d1 = 10 - 6 = 4, d2 = 10 - 4 = 6
et
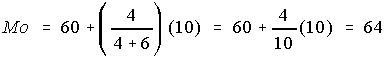
Ce qui est relativement proche du «vrai» mode, c'est-à-dire Mo = 65
La médiane est la valeur calculée (pas nécessairement observée) pour laquelle la moitié de l’effectif de l’échantillon est situé en dessous (et, symétriquement, au-dessus) de cette valeur. Dans un échantillon de n individus trié par ordre croissant de valeur, la médiane est la valeur de (((n/2) -1)+ ((n/2)+1))/2 si n est pair (valeur calculée) ou celle du N/2 ème individus de l’effectif classé, si l’échantillon est impair (valeur observée).
Autre définition:
La médiane est la valeur qui sépare une série d'observations ordonnées en ordre croissant ou décroissant, en deux parties comportant le même nombre d'observations.
Si N est impair,
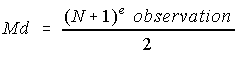
dans le rangement ascendant (ou descendant)
Exemple: Soient les données suivantes: 34, 37, 40, 41, 44, 44, 45, alors
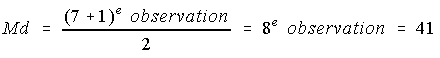
Si N est pair
la médiane correspond au point milieu (ou la moyenne) des deux observations centrales dans le rangement ascendant (ou descendant)
En formule, soit N = 2K, donc K = N/2; alors
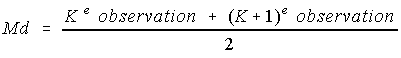
Exemple: Pour les notes du professeur Lecompte, il y a N = 30 observations.
Par conséquent, K = 30/2 = 15 et, dans le classement ascendant,
la 15e valeur était 65 et la 16e valeur était aussi 65, d'où
Étapes
La formule est
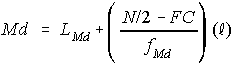
où
Exemple
La classe médiane est celle qui contient le quinzième
élève.
À partir de la distribution de fréquences cumulées, on
observe qu'il s'agit de la classe «60 et moins de 70»; donc
Dans ce cas-ci, l'approximation est «exacte» puisque la «vraie» médiane est aussi Md = 65
EXEMPLE Récapitulatif
Les nombres ci-dessous représentent le nombre d'enfants dans chacune des dix familles choisies au hasard :
Moyenne
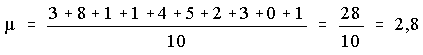
Médiane
Rangeons les données en ordre ascendant
Mode
On voit immédiatement que Mo = 1
On remarque que les trois mesures sont différentes.
Laquelle est la plus «représentative» ?
Le calcul du quartile relève du même procédé que celui de la médiane, à ceci près que l’on considère une partition de la population ordonnée (par ordre croissant) en 4 ensembles égaux (25%).
Le premier quartile est la valeur pour laquelle 25% de l’effectif de l’échantillon est égal ou inférieur à cette valeur (observée ou calculée, même principe que pour la médiane).
Le second quartile correspond à la valeur séparant l’effectif de l’échantillon en 2 lots égaux = c’est également la médiane.
Le troisième quartile est la valeur pour laquelle 75% de l’effectif est égal ou inférieur à cette valeur (et 25% au dessus, donc).
Dans le cas de déciles, le premier décile correspond à la valeur pour laquelle 10% de l’effectif de l’échantillon est égal ou inférieur à cette valeur. Etc.
Il en est de même du centile où l’on considère la nième fraction du centième de l’effectif.
Quartile, décile et centiles sont très utilisé pour les statistiques économiques afin de caractériser la distribution d’une ressource dans une population : par erxemple, 10% de la population monopolise 90% des richesses ou 20% de la populationb produit 80% de la population.
La dispersion est une propriété fondamentale de la variabilité. Elle est cependant difficile à évaluer de façon empirique et nécessite le passage par des calculs souvent complexes.
Paramètre de dispersion le plus intuitif. Facile à calculer, son utilité est limitée. L’étendue est la différence entre la valeur maximale observée de l’échantillon et la valeur minimale.
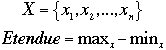
Définition:
L'écart moyen, noté EM, est la moyenne des écarts absolus entre chaque observation et la moyenne des observations.
Étapes
La formule générale est
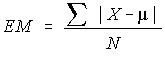
où
Exemple
Voir le tableau de calcul ci-dessous :
| X | µ | | X-µ| |
| 68 | 66,23 | 1,77 |
| 74 | 66,23 | 7,77 |
| 42 | 66,23 | 24,23 |
| 47 | 66,23 | 19,23 |
| 50 | 66,23 | 16,23 |
| 65 | 66,23 | 1,23 |
| 52 | 66,23 | 14,23 |
| 41 | 66,23 | 25,23 |
| 57 | 66,23 | 9,23 |
| 65 | 66,23 | 1,23 |
| 78 | 66,23 | 11,77 |
| 66 | 66,23 | 0,23 |
| 49 | 66,23 | 17,23 |
| 59 | 66,23 | 7,23 |
| 60 | 66,23 | 6,23 |
| 55 | 66,23 | 11,23 |
| 61 | 66,23 | 5,23 |
| 72 | 66,23 | 5,77 |
| 56 | 66,23 | 10,23 |
| 79 | 66,23 | 12,77 |
| 88 | 66,23 | 21,77 |
| 68 | 66,23 | 1,77 |
| 90 | 66,23 | 23,77 |
| 63 | 66,23 | 3,23 |
| 69 | 66,23 | 2,77 |
| 81 | 66,23 | 14,77 |
| 87 | 66,23 | 20,77 |
| 65 | 66,23 | 1,23 |
| 85 | 66,23 | 18,77 |
| 95 | 66,23 | 28,77 |
| 1987 | 345,93 |
On a donc
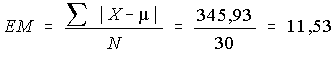
Il s’agira ici de
considérer comment la dispersion se fait par rapport à l’un
des paramètres de position comme la moyenne. On peut, par exemple
considérer l’écart à la moyenne comme étant
la différence 
pour la population et 
pour un
échantillon. Ce principe, étendu à l’ensemble
complet (population ou écantillon donnerait respectivement :
et 
Ce résultat, peu
informatif et inutilisable par la suite, a amené à chercher une
autre expression de l’écart à la moyenne en
considérant cette fois le CARRE de l’écart à la
moyenne soit : 
et 
La somme de ces
carré des écarts à la moyenne (ou SCE) s’exprime :
pour une population et par 
pour un échantillon
Ceci constitue un premier paramètre de dispersion. Cependant, il est peu informatif car il varie en fonction de l’écart à la moyenne mais, surtout, en fonction du nombre de représentants constituant la population ou l’échantillon. On a donc proposé une expression qui ajuste la variation due à la dimention de l’ensemble
considéré (population ou échantillon) et on obtient ainsi la
variance qui s’exprime, pour la populati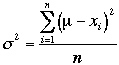on 
et pour un
échantillon :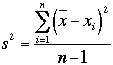 
Récapitulation des Étapes
La variance s’exprime dans une unité qui est le carré de l’unité de la variable de départ : par exemple en kg2 si la variable était une masse exprimée en kg. Son utilisation n’est pas toujours facilement interprétable.
L’écart type
permet de ramener la dispersion exprimée par la variance à une unité connue : la
variance correspond au carré de l’erreur attendue (xpected) par
rapport à la moyenne. En extrayant la racine carrée nous obtiendront
l’écart type. Celui-ci s’exprime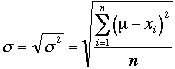 
pour une
population et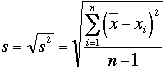 
pour un échantillon.
La formule générale est :
où :
Évidemment, on a :
et la formule «simplifiée» :
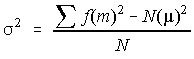
Exemple
Résultat |
Nombre (f) |
Centre (m) | fm |
Écarts m-µ |
(m-µ)2 |
f(m-µ)2 |
| 40 et moins de 50 | 4 | 45 | 180 | -21,33 | 454,97 | 1819,88 |
| 50 et moins de 60 | 6 | 55 | 330 | -11,33 | 128,37 | 770,22 |
| 60 et moins de 70 | 10 | 65 | 650 | -1,33 | 1,77 | 17,70 |
| 70 et moins de 80 | 4 | 75 | 300 | 8,67 | 75,17 | 300,68 |
| 80 et moins de 90 | 4 | 85 | 340 | 18,67 | 348,57 | 1394,28 |
| 90 et moins de 100 | 2 | 95 | 190 | 28,67 | 821,97 | 1643,94 |
| S | 30 | 1990 | 5946,70 |
d'où :
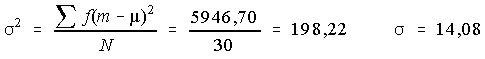
qu'on peut comparer avec la valeur «exacte» = 14,24
Pour comprendre le principe de l’inégalité de Tchebycheff, il faut faire appel à une compréhension intuitive des probabilités. L’inégalité de Tchebycheff correspond à la probabilité que, dans une population, une valeur x, distante de k écarts types de la moyenne de cette population est inférieure ou égale à 1 moins 1 divisé parle carré dek , soit :
Jusqu'ici, les mesures de dispersion présentées sont des mesures dites absolues. Considérons maintenant une mesure de dispersion relative.
Objectif:
Dans certaines situations, on désire comparer le taux de
dispersion de distributions alors que leurs échelles de mesure respective ne sont pas comparables.
L'objectif du coefficient de variation est de fournir un indice quantitatif permettant cette comparaison.
Définition : :
Le coefficient de variation, noté CV, correspond à l'écart type de la distribution exprimé en pourcentage de la moyenne de la distribution. La formule générale est :
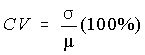
Exemple:
Pour les données du cours de comptabilité, on a obtenu µ = 66,23 et s = 14,24; donc
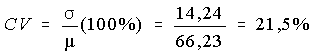
À titre de comparaison, si la note finale avait été calculée sur 10, on aurait obtenu µ = 6,623 et s = 1,424, mais quand même
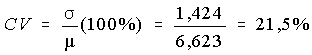
La forme d'une distribution correspond à la capacité de superposer le contour d’un histogramme de fréquence (de la distribution d’un échantillon) avec la courbe retraçant la fonction théorique de distribution, normale ou non. D’une façon schématique, la forme d’une courbe peut être définie par la symétrie de la distribution par rapport à un paramètre de position comme la moyenne, ou par un aplatissement plus ou moins important.
Il est intéressant de définir si un jeu de données présente des déviations par rapport à la moyenne plus fréquentes dans un sens ou l’autre (plus faible ou plus fort que la moyenne). Lorsque la répartition des effectifs se fait de façon symétrique par rapport à la moyenne, la distribution est symétrique. Lorsque l’effectif est plus important pour les valeurs supérieures à la moyenne, on aura une asymétrie positive, dans l’autre cas une asymétrie négative. Il est possible de calculer un coefficient d’asymétrie pour chaque distribution. Le plus couramment employé est celui de Fisher. C’est le moment central d’ordre 3 de la moyenne par rapport à l’écart type (la variance est le moment d’ordre 2).
Pour une population, il
est : 
.
Pour un échantillon :
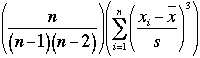
Dans une distribution normale l’asymétrie est nulle. On considérera que l’on ne peut rejeter l’hypothèse de normalité de la distribution (pour alpha = 0,05) lorsque ce paramètre est compris entre -2 et +2.
Ce coefficient est calculé par la plupart des programme d’analyse statistique descriptive.
Dans EXCEL, utiliser la formule COEFFICIENT.ASYMETRIE (xx :yy) ou xx désigne la première case contenant les valeurs de la distribution à tester et yy la dernière case.
Le tableau ci-dessous définit la valeur de l'asymétrie pour quelques distributions courantes.
L’aplatissement mesure l’extension (heaviness) des limites latérales d’une population (tails). On peut également considérer que ce paramètre traduit le "relief" de la distribution. Parmi les formules permettant de calculer ce paramètre, celle de Fisher est la plus fréquemment utilisée. C’est le moment central d’ordre 4 de la moyenne par rapport à l’écart type.
Pour une population :
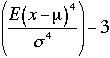
Pour un
échantillon :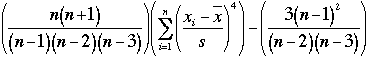 
Dans une distribution normale l’aplatissement est nul. On considérera que l’on ne peut rejeter l’hypothèse H0 de normalité de la distribution (pour alpha = 0,05) lorsque ce paramètre est compris entre -2 et +2.
Ce coefficient est calculé par la plupart des programme d’analyse statistique descriptive.
Dans EXCEL, utiliser la formule KURTOSIS (xx :yy) ou xx désigne la première case contenant les valeurs de la distribution à tester et yy la dernière case.
Le tableau suivant évalue l'aplatissement de Fisher pour quelques distributions courantes.
