STATISTIQUES A UNE DIMENSION.

Pourquoi étudier un échantillon tiré d’une population plutôt que la population dans son intégralité?
|
Ressource illimitée: |
Données disponibles limitées: |
Expérimentation destructive: |
|
n tend vers l'infini |
1 médecin: comparer survie après chirurgie cardiaque entre hommes et femmes |
étude du poids du cerveau des lapins: impossible de tuer tous les lapins et d'en extraire le cerveau |
|
Prendre toutes les chauve-souris de la planète? |
L'analyse qui suit est purement
DESCRIPITVE: pas de conclusions tirées sur la population.LE CLASSEMENT DES DONNEES:
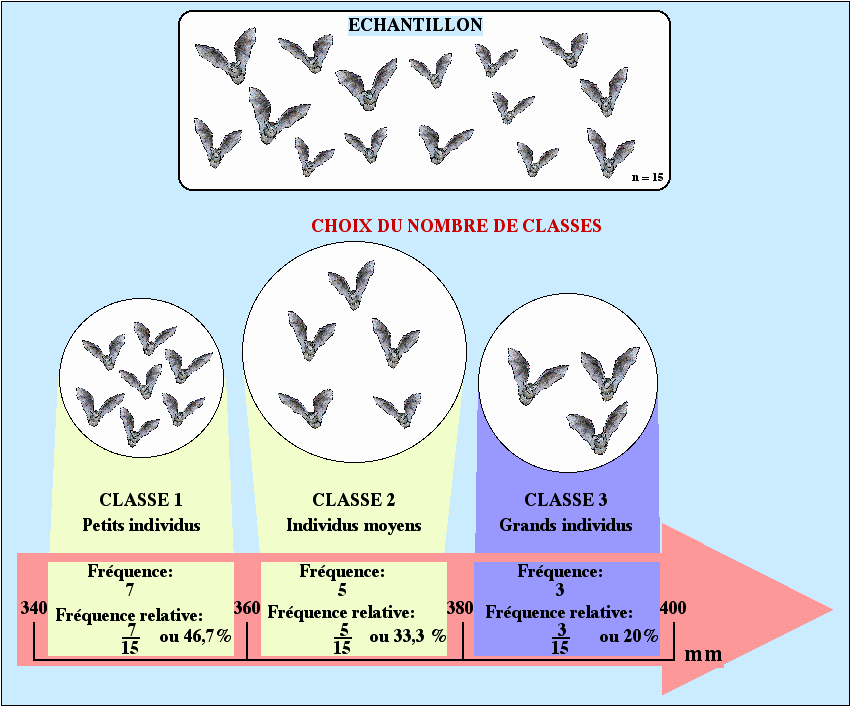
TABLEAU DE FREQUENCES:
|
Fréquences ni |
n1=7 |
n2= 5 |
n3=3 |
n = 7+5+3 = 15 |
|
Fréquences cumulées S ni |
7 |
7+5=12 |
12+3=15 |
|
|
Fréquences relatives |
|
|
|
|
|
Fréquences relatives cumulées |
0,47 |
0,8 |
1 |
LES MESURES DE TENDANCE CENTRALE
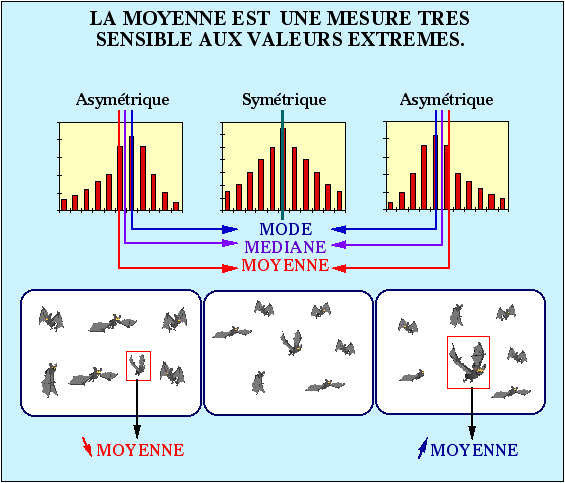
Parmi les mesures de tendance centrale, figurent la moyenne arithmétique, le mode et la médiane.
La moyenne arithmétique est la mesure la plus facile à calculer (somme de toutes les mesures de l’échantillon divisée par le nombre d’observation de l’échantillon) mais aussi très sensible aux valeurs extrêmes (voir: comparaison entre moyenne, médiane et mode).
Le mode détermine la valeur la plus fréquente dans un échantillon. Si l’échantillon est divisé en classes, la classe modale constitue la classe la plus fréquente.
La médiane est la valeur telle que 50% des observations de l’échantillon lui sont inférieures. Si le nombre d’observations est pair, la médiane est la la moyenne entre les observations n/2 et (n+2)/2. Si le nombre d’observations est impair, la médiane est la valeur (n+1)/2.
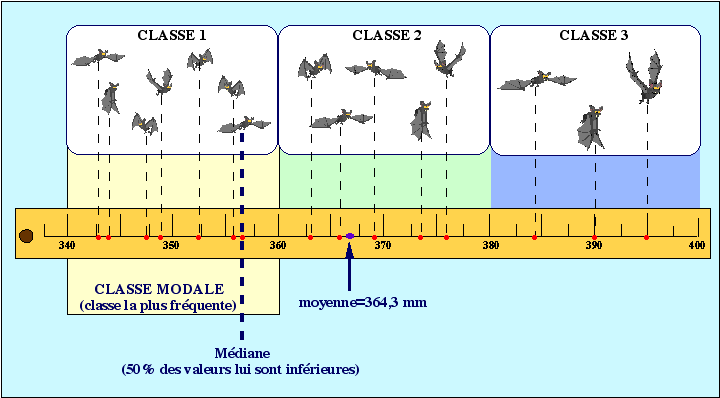
Comparaison entre moyenne, médiane et mode.
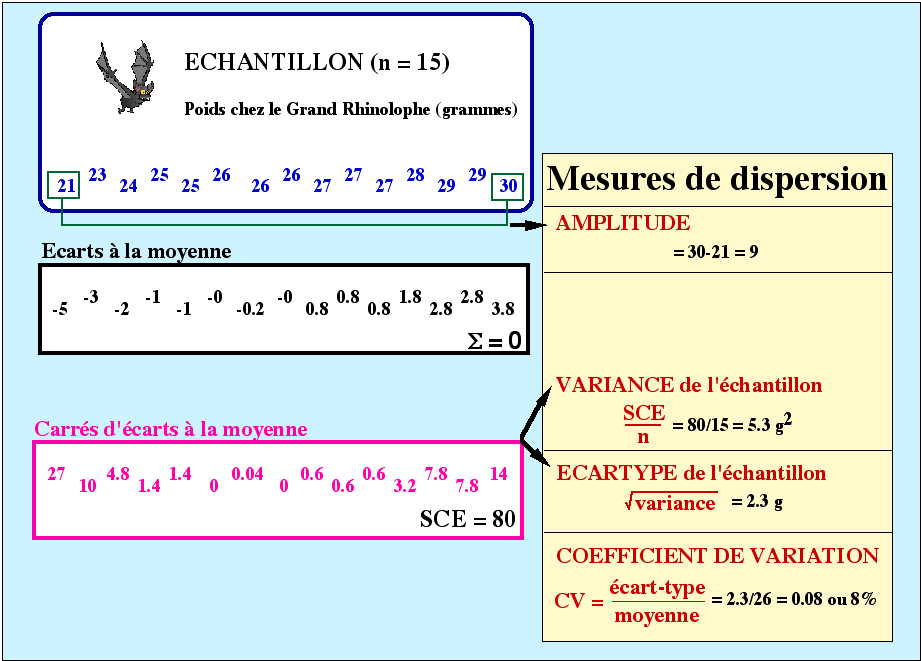
LES MESURES DE DISPERSION.
L’amplitude, la variance, l’écart-type et le coefficient de variation sont des mesures qui rendent compte de la dispersion des valeurs d’un échantillon.
L’amplitude constitue l’écart qui sépare la valeur la plus petite d’un échantillon par rapport à la plus grande.
La variance reflète la façon dont les valeurs de l’échantillon oscillent autour de la moyenne. Elle est exprimée dans le carré des unités de la moyenne. Il est obtenu en sommant tous les carrés d’écarts à la moyenne pour chacun des individus de l’échantillon (SCE somme de carrés d’écarts) puis en divisant cette SCE par la taille de l’échantillon n. La mise au carré des écarts est indispensable. Elle évite les signes pour les écarts à la moyenne (de plus la somme des écarts est nulle. Ce qui est peu informatif). Remarquons que la SCE divisée par n estla variance de l’échantillon. A ne pas confondre avec la SCE divisée par n-1 qui constitue l’estimateur de la variance de la population. Ce dernier constitue une approximation de la variance de la population mais pas LA variance de la population (
s2) inconnue.La variance est souvent peu commode à visualiser et on lui préfère l’écart-type. Il est obtenu en effectuant la racine carrée de la variance. Il est exprimé dans les unités de la moyenne.
Le coefficient de variation permet d’apprécier la précision d’un instrument de mesure scientifique. Lorsqu’il tend vers 0, cela signifie que les observations de l’échantillon sont très proche de la moyenne. Au contraire, lorsque le coefficient tend vers 1 ( ou 100%) ou est supérieur à 1, cela implique que les données sont très éloignées de la moyenne.