4.3. Cas de k échantillons

4.3.1. Cas de k échantillons appariés

Ces tests permettent la comparaison de plus de deux populations apparentées.

Il y a des circonstances dans lesquelles nous devons réaliser un protocole de telle sorte que plus de deux échantillons ou conditions doivent être étudiés simultanément. Dans ces conditions, il est nécessaire d'utiliser un test statistique qui indiquera si une différence globale existe entre les k différentes conditions. Seulement dans ce cas là, sera-t-il justifié d'employer une procédure pour rechercher l'existence de différences significatives entre n'importe quel couple des k échantillons. Il peut ainsi être montré que, pour 5 échantillons, la probabilité qu'une comparaison deux à deux (10 tests) mette en évidence une différence significative ou plus au seuil 0,05 est en fait p = 0,40. Des cas, où le test global sur 5 échantillons concluait à un résultat non significatif mais où la comparaison deux à deux des 5 échantillons conduisait à des résultats significatifs, ont été rapportés dans la littérature. Aussi aucune confiance ne peut être accordée lorsque la décision concernant k échantillons est prise à la suite d'une comparaison deux à deux des échantillons.
Il est possible d'obtenir k groupes appariés de différentes façons. Les k échantillons de taille égale sont appariés en fonction d'un ou plusieurs critères qui peuvent affecter les valeurs des observations ou l'appariement peut être réalisé en comparant les mêmes individus dans les k conditions.
La technique paramétrique pour tester si plusieurs échantillons sont extraits de populations identiques est l'analyse de variance. Dans le cas de plusieurs échantillons appariés, c'est l'analyse de variance à deux facteurs (Two-way analysis of variance). Si les contraintes de cette technique (observations tirées indépendamment de populations normales ; populations ayant la même variance; les moyennes de ces populations sont des combinaisons linéaires des "effets" des colonnes et des lignes) ne sont pas respectées, ou si les variables ne sont pas mesurées dans une échelle d'intervalle, il est possible d'utiliser des techniques statistiques non paramétriques.

4.3.1.1. Test de Cochran pour données binaires (Cochran Q test)

Il permet de tester l'hypothèse que k échantillons appariés de fréquences ou de proportions ont été extrait de la même population, les mesures sont nominales. C'est le cas dans les situations où la réponse d'une unité ne peut être que deux types : oui ou non, gagné ou perdu, succès ou échec, vivant ou mort, mâle ou femelle... Chacune des réponses sera noté 0 ou 1.

Prenons comme exemple, trois ascensions différentes sont tentées par cinq membres d'un club d'alpinisme. Les succès seront enregistrés comme un 1 et les échecs comme un 0. Chacun des 5 alpinistes aura tenté les ascensions. On peut construire un tableau de k colonnes (ou traitements) et N lignes (sujets).

Traitements Sujets	Ascension 1	Ascension 2	Ascension 3
A	1	1	0	2	4
B	1	0	1	2	4
C	0	0	1	1	1
D	0	1	1	2	4
E	1	0	1	2	4
	3	2	4	=9	=17

G_j = Nombre total de succès (1) dans la jème colonne, G₁=3, G₂ = 2, G₃ = 4.
L_i = Nombre total de succès (1) dans la ième ligne, L₁= 4, L₂ = 4, L₃ = 1, L₄ = 4, L₅ = 4.
k = nombre de traitements, 3 .
N = nombre de sujets testés, 5.
H₀ = les ascensions présentent la même difficulté.
H₁ = les difficultés des ascensions sont significativement différentes.

Cochran (1950) a montré que si les succès et les échecs sont distribués aléatoirement dans les lignes et les colonnes (H₀), alors si le nombre de lignes n'est pas trop faible :

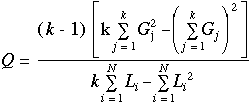
la distribution exacte de Q s'approche de celle du c² à k - 1 degrés de liberté en cas de grands échantillons (Table 2).

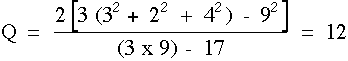Conclusion:
Notre valeur Q est supérieure à la valeur critique du c² à 2 degrés de liberté au seuil 0,05 (= 5,99 ; Table 2), nous rejetons l'hypothèse nulle et nous concluons que les difficultés des 3 ascensions sont significativement différentes.

4.3.1.2. Analyse de variance de Friedman (Friedman two-way analysis of variance)

Il permet de tester l'hypothèse que k échantillons ont été extrait de la même population. Les k échantillons ne sont pas indépendants, et de ce fait, le nombre de cas doit être le même dans chacun des échantillons. La non indépendance peut être obtenue en étudiant le même groupe dans chacune des k conditions. Ou bien, il est possible de constituer différents ensembles, chacun composé de k sujets apparié, puis d'assigner au hasard un sujet de chaque ensemble à une condition, un autre sujet de chaque ensemble à la seconde condition....
Ce test distribue les données en un tableau à double entrée ayant N rangées et k colonnes. Les rangées représentent les différents sujets et les colonnes les différentes conditions. Les données sont rangées. La détermination des rangs se fait pour chaque rangée séparément. Donc pour k conditions, les rangs de chaque rangée se répartissent entre 1 et k. Le test détermine si les différentes colonnes de rangs proviennent de la même population.

Supposons que l'on veuille étudier les résultats de 3 groupes dans 4 conditions. Chaque groupe contient 4 sujets appariés, un ayant été assigné à chacune des quatre conditions. Les résultats sont présentés dans le tableau suivant :

On commence par ranger les données dans chaque ligne. On obtient alors le tableau suivant :

Si l'hypothèse nulle (que tous les échantillons, colonnes, proviennent de la même population) est vraie, la distribution des rangs dans chaque colonne sera due à la chance, et les différents rangs apparaîtront avec le même fréquence. Le total des rangs par colonne (Rj) sera aléatoire. Mais, si les observations sont dépendantes d'au moins une des conditions (si H₀ est fausse), alors le total des rangs par colonnes devrait varier d'une colonne à l'autre. Le test de Friedman teste si le totaux des rangs par colonne différent significativement. La valeur statistique du test est c² r.
Cette valeur se calcule de la façon suivante :

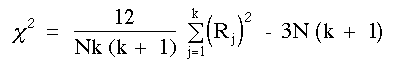(17)

où N = nombre de lignes ; k = nombre de colonnes ; Rj somme des rangs de chaque colonne ;

somme des carrés de la somme des rangs de toutes les colonnes.

Comme la distribution d'échantillonnage du c²r est une approximation de la distribution du khi carré à k - 1 degré de liberté, la probabilité associée à l'obtention de valeurs aussi élevée que celle du c²r observée est donnée par la table 2. Si la valeur du c²r calculée par la formule (17) est égale ou supérieure à celle donnée dans la table 2 pour un niveau de signification et un degré de liberté donnés, les sommes des rangs des diverses colonnes diffèrent significativement et H₀ peut être rejeté.
Lorsque le nombre de colonnes ou/et le nombre de lignes est trop faible, il faut utiliser les tables 10 qui donnent les probabilités exactes associées au c²r observé pour k = 3, N = 2 à 9, et pour k = 4, N =2 à 4.

Pour illustrer le calcul du khi carrér et l'utilisation des tables 10, utilisons les données de l'exemple précédent. Les sommes des rangs par colonne était de 11, 5, 4 et 10. k = 4 ; N = 3. Calculons le c²r en substituant ces valeurs dans la formule (17).

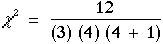[ (11)2 + (5)2 + (4)2 + (10)2] - (3) (3) (4 + 1) = 7,4

Par référence à la table 10, la probabilité exacte associée à c²r égal ou supérieur à 7,4 ; quand k = 4 et N = 3 ; est p = 0,033. Nous pouvons donc rejeter H₀ au seuil 0,033.

Exemple lorsque N et k sont importants

Lors d'une étude de l'effet de trois canevas différents de renforcement sur la qualité de l'apprentissage chez le rat, trois échantillons appariés (k = 3) de 18 rats (N = 18) furent soumis à trois patrons différents de renforcement. L'appariement fut obtenu en prélevant 3 jeunes d'une même portée dans 18 portées différentes. Bien que les 54 rats reçurent la même quantité de renforcement (récompense), l'administration des récompenses différa pour chaque groupe. Un groupe reçu une récompense après chaque essai réussi (RR). Le deuxième et le troisième groupe furent soumis à un renforcement partiel, et chaque séquence d'essais se terminait par un essai sans récompense pour le deuxième (RU) alors qu'il se terminait par un essai récompensé pour le troisième groupe (UR). Après cet entraînement, la qualité de l'apprentissage fut mesurée par la vitesse à laquelle les rats apprenaient une règle "opposée", alors que les rats avaient été entraînés à courir en direction d'une cible blanche, les rats étaient récompensés pour courir en direction d'une cible noire. Plus la qualité de l'apprentissage initial etait bonne, plus le transfert d'apprentissage devrait être difficile. L'expérimentateur prédisait que les différents modes de renforcements résulteraient en des apprentissages secondaires différents.


L'hypothèse nulle pose que les différents modes de renforcement n'ont aucun effet différenciateur sur l'apprentissage ultérieur. L'hypothèse alternative pose que les différents canevas de renforcement ont un effet différenciateur.

Soit un seuil de signification de a = 0,05 et N = 18 = le nombre de rats dans chacun des 3 groupes appariés.

L'analyse de variance non-paramétrique de Friedman est choisie plutôt qu'une analyse paramétrique car les nombres d'erreurs mesurés ne le sont probablement pas dans une échelle d'intervalle. De plus, les valeurs obtenues semblent indiquer une absence d'homogénéité des variances suggérant que les hypothèses du test de F ne sont probablement pas respectées.

La distribution d'échantillonnage est approximativement celle du khi carré avec un degré de liberté = k - 1 et pour N et/ou k important. Aussi la probabilité associée à la valeur observée peut être déterminée par référence à la table 2.

Le domaine de rejet est constitué par toutes les valeurs de c²r dont la probabilité associée est égale ou inférieure au seuil de signification choisi.

Le nombre d'erreurs commis par chaque rat lors du second apprentissage fut déterminé, et ces valeurs furent rangées pour chacun des 18 ensemble de 3 rats appariés. Ces rangs sont donnés dans la table ci-dessous.

Le total des rangs dans le lot RR est de 39,5, celui du lot RU est de 42,5, et celui du lot UR est de 26,0. Un rang faible signifie que les rats ont commis de nombreuses erreurs lors du deuxième apprentissage et donc indique que l'apprentissage initial était de bonne qualité.

Nous pouvons calculer la valeur du khi carré r en substituant nos valeurs observées dans la formule 17.



	Mode de renforcement
Groupe	RR	RU	UR
1	1	3	2
2	2	3	1
3	1	3	2
4	1	2	3
5	3	1	2
6	2	3	1
7	3	2	1
8	1	3	2
9	3	1	2
10	3	1	2
11	2	3	1
12	2	3	1
13	3	2	1
14	2	3	1
15	2,5	2,5	1
16	3	2	1
17	3	2	1
18	2	3	1
Rj	39,5	42,5	26,0







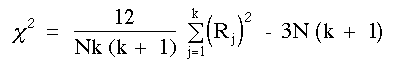
[ (39,5)2 + (42,5)2 + (26,0)2 ] - (3) (18) (3 + 1)


c²r = 8,4


En se référant à la table 2, un c²r = 8,4 et un degré de liberté = k -1 = 3 - 1 = 2 est significatif au niveau de signification 0,02 et 0,01. Comme p < 0,02 est inférieur au seuil de signification choisi a = 0,05, notre décision est de rejeter H₀. La conclusion est que les performances des rats au second apprentissage dépendent du mode de renforcement appliqué lors de l'apprentissage initial.

Dans le groupe 15, les animaux RR et RU ont obtenu les mêmes scores et sont donc ex-aequo pour les rangs 2 et 3. Ils ont reçu tous les deux le même rang 2,5, la moyenne de la somme des rangs. Friedman affirme que la substitution du rang moyen pour les valeurs ex-aequo n'affecte pas la validité du test du khi carré r.

Si le test de Friedman conclut à un résultat globalement significatif, on peut tester la signification de comparaisons choisies, en étudiant les différences entre les sommes ou moyennes de rangs des traitements.

On juge significatives des différences de sommes de rangs supérieures à la plus petite différence significative données par :

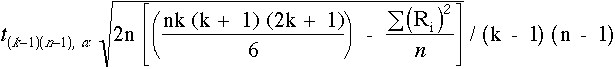(B)

Exemple avec un grand échantillon :
Puisque n = 18 et k = 3, la distribution t a 34 degrés de liberté, nous trouvons dans les tables que t _{34; 0,05} = 2,033. La plus petite différence est alors de : application de la formule (B)

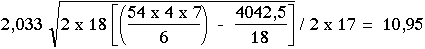La somme des rangs de chacun des traitements est : RR = 39,5 ; RU = 42,5 ; UR = 26,0.
Nous en déduisons les deux différences supérieures à 10,95 : RR - UR = 13,5 et RU - UR = 16,5

Nous concluons que les deux premiers apprentissages initiaux étaient de moins bonne qualité que le troisième apprentissage initial. Ou, le mode renforcement appliqué au cours du troisième apprentissage est le meilleur.

Exemple avec le petit échantillon
n = 3 ; k = 4 ; ddl = 6 ; table des t _{6 ; 0,05} = 2,447
La plus petite différence est alors (application de la formule (B) = 3,998.
Les sommes des rangs de chacune des conditions sont :
Condition I = 11 ; CII = 5 ; C III = 4 ; C IV = 10. Les quatre différences supérieures à 3,998, sont : CI - CII = 6 ; CI - CIII = 7 ; CIV - CII = 5 ; CIV - CI = 6.
Nous concluons que les résultats obtenus dans les conditions I et IV sont significativement supérieurs à ceux des conditions II et III.

Un autre test, le test Q de Cochran permet de tester si trois ensembles appariés de fréquences ou plus diffèrent significativement entre eux. Il est spécialement adapté lorsque les données sont mesurées dans une échelle nominale ou ordinale.

4.3.2. Cas de k échantillons indépendants

Les tests non paramétriques permettant de tester si des échantillons indépendants, non nécessairement de même taille, sont tirés de populations identiques sont des analyses de variance à un facteur (One-way analysis of variance).

4.3.2.1. Test du khi carré pour k échantillons indépendants

Il permet de déterminer la signification des différences entre k groupes indépendants, lorsque les données sont des fréquences. C'est une extansion du khi carré pour deux échantillons indépendants et se calcule de la même façon.
Les fréquences doivent être arrangées dans une table k x r, où k = nombre de colonnes (groupes) et r = nombre de lignes. L'hypothèse nulle (les k échantillons ne diffèrent pas entre eux) peut être testée en utilisant la formule 7 :

(7)

où Oij = nombre de cas classé dans les i rangées et les j colonnes.
Tij = nombre de cas attendus, classés dans les i rangées et les j colonnes.

La distribution d'échantillonnage du c² calculé par la formule 7, sous H₀, se rapproche d'une distribution khi carré avec un degré de liberté = (k -1) (r -1). La table 2 donne alors la probabilité associée au khi carré observé. Lorsque la valeur observée du khi carré est égale ou supérieure à celle de la table à un niveau de signification et pour un degré de liberté donnés, alors H₀ peut être rejeté.

Exemple
Lors d'une étude sur la nature et les conséquences de la stratification sociale dans une petite ville du centre-Ouest des Etats-Unis d'Amérique, Hollingshead montra que les membres de cette communauté se répartissaient eux-mêmes en 5 classes sociales. Son étude était centrée sur les corrélats de cette stratification parmi les jeunes. L'une de ses prédictions était que les adolescents des différentes classes sociales s'engageaient dans différentes voies d'étude (général, commercial, préparation à l'université) au lycée de la ville. Cette hypothèse fut testée en identifiant l'appartenance sociale de 390 lycéens et en déterminant leur choix scolaire.
L'hypothèse nulle pose que la proportion de lycéens inscrit dans chacune de trois filières alternatives est la même dans chaque classe sociale. Pour l'hypothèse alternative, la proportion de lycéens inscrit dans chaque filière diffère suivant les classes sociales.
Le khi carré convient pour traiter ce type de données discrètes. Le tableau suivant donne les résultats de cette étude.

Les classes sociales I et II sont regroupées du fait de la faiblesse de leurs effectifs.
En italique, apparaissent les fréquences théoriques des inscriptions dans les trois filières, lorsque H₀ est vraie. Elles sont calculées, pour chaque cellule du tableau, par le produit des totaux marginaux de cette cellule divisé par le total général.
Le calcul du khi carré est le suivant :

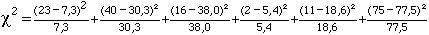
c² = 33,8 + 3,1 + 12,7 + 2,1 + 3,1 + 0,08 + 1,0 + 0,003 + 7,3 + 1,4 + 3,1 + 1,5

c² = 69,2

Le degré de liberté est égal à (k -1)(r -1) = (4 - 1)(3 - 1) = 6. La table 2 pour un ddl de 6 révèle que le khi carré observé est significatif au-delà du niveau 0,001, l'hypothèse nulle peut être rejetée au seuil 0,01. Les filières d'enseignement choisies par les lycéens ne sont pas indépendantes de l'appartenance à une classe sociale dans cette petite ville.
On retrouve la contrainte que moins de 20% des cellules du tableau doivent avoir une fréquence théorique inférieure à 5 et aucune inférieure à 1. Dans le cas contraire, il est possible de regouper des catégories adjacentes, mais à condition que ces catégories aient une quelconque propriété commune. La meilleure façon d'éviter ce problème de regoupement est de travailler avec un effectif suffisamment important.
Il n'existe pas d'alternative à ce test.

4.3.2.2. Extension du test des médianes (extension of the median test)

Ce test détermine si k groupes indépendants ont été extraits de la même population ou de populations ayant des médianes égales. Les variables doivent être mesurées au moins dans une échelle ordinale.

Méthode
Le test nécessite le calcul de la médiane de l'ensemble des observations. Chaque valeur est alors remplacée par un plus (+) si elle est supérieure à la médiane globale et par un moins (-) lorsqu'elle est inférieure ou égale à la médiane globale. Le dénombrement des valeurs inférieures et supérieures à la médiane commune permet d'établir un tableau de contingence k x 2, puis de réaliser un test du khi carré avec la formule 7.
Le degré de liberté est (k - 1) (r - 1), mais comme le nombre de lignes est de 2 le degré de liberté est alors égal à
ddl = (k -1) (r -1) = (k -1) (2 -1) = (k -1).
Lorsque les valeurs se répartissent exactement de part et d'autre de la médiane commune, la fréquence théorique des cellules d'une colonne est la moitié du total marginal de cette colonne. Lorsque la répartition se fait entre les valeurs supérieures à la médiane commune et les autres, les fréquences théoriques se calculent de la même façon que pour le khi carré.
Quand les données ont été réparties en plus et en moins par rapport à la médiane commune, et que les fréquences correspondantes ont été distribuées dans un tableau k x 2, la procédure de calcul est la même que celle utilisée pour le khi carré pour k échantillons indépendants.

Exemple
Supposons qu'un chercheur veuille étudier l'influence du niveau d'instruction des mères sur le degré d'intérêt qu'elles présentent pour la scolarité de leurs enfants. Le niveau d'instruction de chaque mère est apprécié par le diplôme le plus important obtenu par chacune d'elle et leur degré d'intérêt pour la scolarité des enfants est mesuré par le nombre de visites volontaires que chacune d'elle rend à l'école. En tirant au hasard un nom sur dix d'une liste de 440 enfants inscrit à l'école, il obtient les noms de 44 mères, qui constituent son échantillon. Son hypothèse est que le nombre de visites varie en fonction du niveau d'éducation des mères.
Comme les groupes de mères de divers niveau d'instruction sont indépendants les uns des autres et que plusieurs goupes sont formés, un test pour k échantillons indépendants est envisagé. Comme le nombre d'années de scolarité des mères et que le nombre de visites constituent au mieux des mesures ordinales du niveau d'instruction et du degré d'intérêt, le test des médianes est considéré comme le mieux adapté à tester l'hypothèse concernant des différences des tendances centrales.
Soit a = 0,05 ; N = 44, le nombre de mères de l'échantillon; le degré de liberté = k -1 puisque r = 2. Les résultats obtenus dans cette étude fictive sont dans le tableau suivant.

Nombre de visites à l'école

La médiane commune pour ces 44 valeurs est de 2,5. C'est-à-dire que la moitié des mères ont rendu visite à l'école deux fois ou moins et l'autre moitié trois fois ou plus. Le tableau de contingence donne le nombre de mères pour chaque niveau d'éducation qui ont rendu un nombre de visites inférieur ou supérieur à la médiane commune. Ce tableau est le suivant où les valeurs en italique indiquent les fréquences théoriques.

Tableau de contingence

Les données présentées sous cette forme ne sont pas traitable par le khi carré, car plus de 20% des cellules du tableau ont une fréquence théorique inférieure à 5. Les catégories ayant des fréquences attendues insuffisantes sont celles concernant les mères ayant été à l'université un nombre plus ou moins grand d'années. Il est alors justifié de regrouper ces trois catégories en une seule : niveau universitaire. De cette façon nous obtenons le tableau suivant :

Les données se présentent alors sous une forme compatible avec une analyse du khi carré. Nous pouvons alors calculer la valeur du khi carré à l'aide de la formule 7.

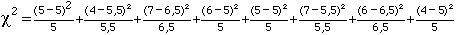
c²= 0 + 0,409 + 0,0385 + 0,2 + 0 + 0,409 + 0,0385 + 0,2

c²= 1,295

Comme le degré de liberté est de 3, la table 2 révèle que la probabilité d'avoir une valeur de khi carré égale ou supérieure à 1,295 est comprise entre 0,80 et 0,70. Cette probabilité étant supérieure au seuil de signification choisi (a = 0,05), nous ne pouvons rejeter l'hypothèse nulle de cette étude fictive.

4.3.2.3. Test des rangs de Kruskal et Wallis (Kruskal-Wallis one-way analysis of variance)

C'est une extension du test des rangs à deux échantillons indépendants. Il est nécessaire que les données soient mesurées au moins dans l'échelle ordinale.

Méthode
Comme pour deux échantillons, la réalisation du test est basé sur le classement de l'ensemble des observations par ordre croissant, la détermination du rang de chacune d'elles, et le calcul des sommes des rangs, relatives aux différents échantillons.
A partir de ces sommes, on peut ensuite obtenir la valeur H définie par la formule suivante :

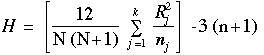(18)

où k = nombre d'échantillons
nj = nombre de cas dans le jème échantillon
N = nj, le nombre de cas pour l'ensemble des échantillons
Rj = somme des rangs dans le jème échantillon (colonne)

=somme des k échantillons.

La quantité H est approximativement une valeur observée d'une variable khi carré à k -1 degrés de liberté, lorsque la taille des différents échantillons n'est pas trop réduite. On doit rejeter l'hypothèse d'identité des k populations, au niveau a, lorsque la valeur H est égale ou supérieure à la valeur du khi carré donné dans la table 2, au seuil de signification choisi et pour k -1 degré de liberté.
L'approximation est satisfaisante lorsque l'on dispose d'une quinzaine d'observations. Pour des effectifs plus réduits (k = 3 et nj≤ 5), les probabilités exactes ont été tabulées (tables 11₁ et 11₂). La première colonne de cette table donne les différentes valeurs possibles de n1, n2 et n3. La seconde colonne donne les différentes valeurs de H et la troisième colonne la probabilité associée. Ainsi, si H est égal ou supérieur 5,8333 pour trois échantillons respectivement de 4, 3 et 1 cas, la table 11₁ indique que l'hypothèse nulle peut être rejetée au seuil de signification 0,021.

Exemple pour de petits échantillons
Supposons qu'un chercheur veuille tester l'hypothèse selon laquelle les administrateurs scolaires sont plus autoritaires que les enseignants. Mais, il sait que certains enseignants aspirent à devenir administrateurs, aussi il décide de diviser ses 14 sujets en trois groupes : les enseignants ne désirant pas devenir administrateurs, les enseignants désirant devenir administrateurs et les administrateurs. Il soumet chacun des sujets à un test mesurant l'autoritarisme. Son hypothèse est que les résultats à ce test des trois groupes diffèreront.
Le tableau suivant donne les résultats du test d'autoritarisme de cette étude fictive :

Les 14 observations sont rangées en ordre croissant :

Nous pouvons alors calculer la valeur de H avec la formule 18.

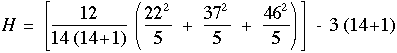
H = 6,4.

La table 11₂, la probabilité d'obtenir un H égal ou supérieur à 6,4, sous H₀, est p < 0,049. Cette probabilité étant inférieure à a = 0,05, notre décision pour cette étude fictive est de rejeter H₀. Nous concluons que les trois groupes d'éducateurs diffèrent par leur autoritarisme.

Observations ex-aequo
Lorsque deux ou plusieurs observations ont la même valeur, chaque observation reçoit la moyenne des rangs des valeurs ex-aequo. La valeur de H peut être influencée par l'existence d'ex-aequo et nécessite l'utilisation d'un facteur correctif. Cependant, dans la plupart des cas, cette correction est sans grande importance. La valeur de H doit être divisée par

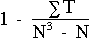(19 )

ou T = t ³- t; t étant le nombre d'observations ex-aequo
N = nombre d'observations de l'ensemble des échantillons, soit N = 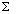nj
T = somme de tous les groupes d'ex-aequo.

Cette correction accroît la valeur de H et rend le résultat plus significatif qu'en absence de la correction.

Exemple pour de grands échantillons
Un chercheur détermina les poids à la naissance des membres de 8 portées différentes de cochons, de façon à vérifier si le poids de naissance est affecté par la taille de la portée.
Le poids de 56 porcelelets provenant de 8 portées différentes sont donnés dans le tableau suivant, ainsi que leur rang dans l'ensemble des mesures.

Nous pouvons calculer la valeur de H non corrigée pour les ex-aequo.

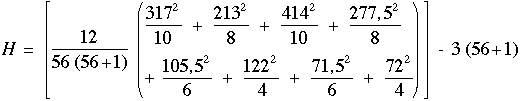
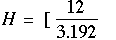(10.048,9 + 5.859,031 + 17.139,6 + 9.625,781 + 1.855,042 + 3.721,0 + 852,042 + 1.296,0)] - 171

H = 18,464

La probabilité d'obtenir un tel H est inférieure à 0,02 (Table 2).
Pour réaliser la correction pour les ex-aequo, il faut d'abord déterminer combien de groupes d'ex-aequo existent et combien d'observations sont égales dans chaque groupe. Les premiers ex-aequo se présentent entre deux porcelets de la portée 7 (qui pèsent 1,2 pounds). Ils reçoivent tous deux le rang 2,5. Dans ce cas t = nombre d'observations liées = 2 ; T = t³ - t = 8 -2 = 6. Le groupe suivant comprend 4 porcelets (portée 1, 2 et 5) et ces observations reçoivent le rang 8,5. Ici t = 4, et T = t³ -t = 64 - 4 = 60. Nous procédons de même pour toutes les valeurs liées et nous trouvons les résultats suivants :

En utilisant la formule 19, nous pouvons calculer la correction totale

= 0,9945

Cette valeur devient le dénominateur du H trouvé précédemment, et le H corrigé pour les ex-aequo est :

H = 18,566

La table 2 montre qu'une telle valeur de H avec un degré de liberté de 7 a une probabilité p < 0,01 (L'analyse de variance paramétrique des mêmes données aboutit à un F = 2,987, qui pour des degré de liberté de 7 et 48, correspond à une probabilité de 0,011). Comme cette probabilité est inférieure au seuil de signification fixé (a = 0,05), nous rejetons H₀. Nous concluons que le poids des porcelets varie de façon significative avec la taille de la portée.
Le test de Kruskal et Wallis est le plus efficace de tous les tests applicable à k échantillons indépendants.

Le test global conclut à une différence significative entre au moins un échantillon et les autres. Il faut donc rechercher la ou les différences significatives.
Nous utiliserons la méthode dite de plus petite différence significative.
Avec le test de Kruskal-Wallis, on décide que les médianes de i-ième et j-ième échantillons diffèrent si les deux critères suivants sont réunis :
1. le test global conclut à une différence significative,
2. l’inégalité suivante est vérifiée :

>

ou et

sont les rangs moyens des deux échantillons comparés (total des rangs de chaque échantillon divisé par n_i ou n_j) ;
est la valeur correspondante de la table de t ; n_i et n_j taille des échantillons, k = nombre d’échantillons ;

N = nombre d'observations de l'ensemble des échantillons, soit

Avec les résultats de l'exemple précédant : N = 56 ; k = 8 ; t_{48 ; 0,05} = 2,0168

Exemples

1. Comparaison 1/7 : différence des rangs moyens dRm = 11,91 > ppds (plus petite différence significative) = 7,20 ; donc la différence entre 1 et 7 est une différence significative.
   
2. Comparaison 2/7 : dRm = 9,75 > ppds = 7,53 ; donc 2/7 différence significative.
   
3. Comparaison 1/8 : dRm = 13,7 > ppds = 10,53 ; 1/8 différence significative.
   
4. Avec l'analyse de variance paramétrique, Staview donne les différences significatives entre les différents échantillons au seuil 0,05 (Fisher PLSD).
   
5. Les moyennes 1, 2, 3, 4, 6 sont significativement différentes de celle de 7 et la moyenne de 3 est significativement différente de celle de 5 et de 8.
   
   
   

   Calculateurs

   Test de Kruskal-Wallis k=3

   Test de Kruskal-Wallis k=4

   Test de Kruskal-Wallis k=5

   Test de Kruskal-Wallis k=6

   Test de Kruskal-Wallis k=7

   Test de Kruskal-Wallis k=8