STATISTIQUES DESCRIPTIVES A DEUX DIMENSIONS.

Les statistiques descriptives à deux dimensions permettent d'étudier deux paramètres pour un même échantillon. Chaque individu de l'échantillon se caractérise donc par deux mesures. Par exemple, pour un échantillon de Grand Rhinolophe, un biologiste a mesuré l'envergure et le poids de chaque individu.
A la différence des statistiques à une dimension, le type de graphique utilisé pour ces deux paramètres est un DIAGRAMME DE DISPERSION. Chaque point représente un individu, et l'ensemble de ces points constitue un nuage de points.
|
|
|
Le but des statistiques à deux dimensions est d'étudier la relation qui existe (si elle existe) entre les deux paramètres étudiés (envergure et poids). Afin de visualiser cette relation, nous devons construire une droite de régression. Elle peut être obtenue en minimisant les écarts des points par rapport à la droite. Celle-ci doit passer, au mieux, par tous les points du nuage de points.
La figure ci-dessous est basée sur le même principe mais correspond aux deux paramètres réduits. Le poids réduit étant obtenu de la façon suivante:
![]()
On procédera de même pour le poids.
![]()
Cette nouvelle subdivision partage le graphique en quatre quadrants. Deux sont positifs car, tous les points contenus dans ces deux quadrants possèdent un produit d'écart à la moyenne de x et y est positif (- par - et + par + donnent +). Les deux autres quadrants sont négatifs car, soit l'écart par rapport à la moyenne des x soit l'écart à la moyenne des y est négatif,rendant ainsi le produit d’écarts négatif (+ par - donne -).
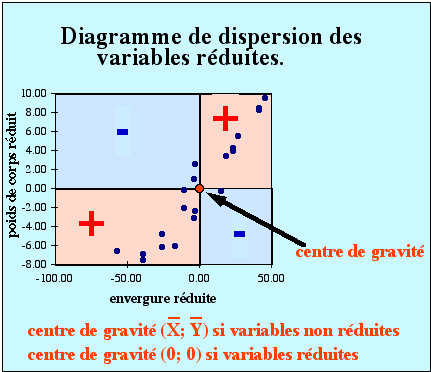
A l'intersection des deux nouveaux axes (moyenne des x, moyenne des y) dans un système non réduit ( (0, 0) pour des axes réduits) se trouve le centre de gravité du nuage de point.
Â
Coefficients:
Le coefficient de corrélation (r)
:Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Pour des valeurs de r 0; -1; +1 on ne peut rien dire sur la linéarité de la relation SANS voir le graphique!
Â
le coefficient de détermination:
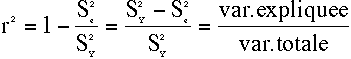
Â
Le carré du coefficient de corrélation s'appelle le
coefficient de détermination (r2).Â
Â
Â
Â
Â
Â
Â
Â
Â
Droites de régression: moindres rectangles ou moindres carrés?
Â
Historiquement, le modèle linéaire a été utilisé en premier lieu pour sa simplicité d'utilisation. Tous les modèles ne sont évidemment pas linéaires mais, dans certains cas, peuvent être linéarisés.
Â
Le calcul de l'équation d'une droite peut se résumer ainsi:
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Â
Si la relation entre les deux paramètres étudiés possède un sens (c'est parce que la température change que la vitesse de réaction chimique change, et pas l'inverse), la droite à utiliser est la
droite des moindres carrés. Au contraire, quand il n'est pas possible d'établir un sens à la relation entre deux paramètres, la droite employée est la droite des moindres rectangles, moins précise que la précédente (ce n'est pas parce que le salaire des enseignants augmentent que leur consommation d'alcool augmente nécessairement. L'inverse n'est pas vrai non plus. Cet accroissement simultané de ces deux paramètres n'est peut-être que la conséquence de l'influence d'un troisième paramètre régissant les deux premiers).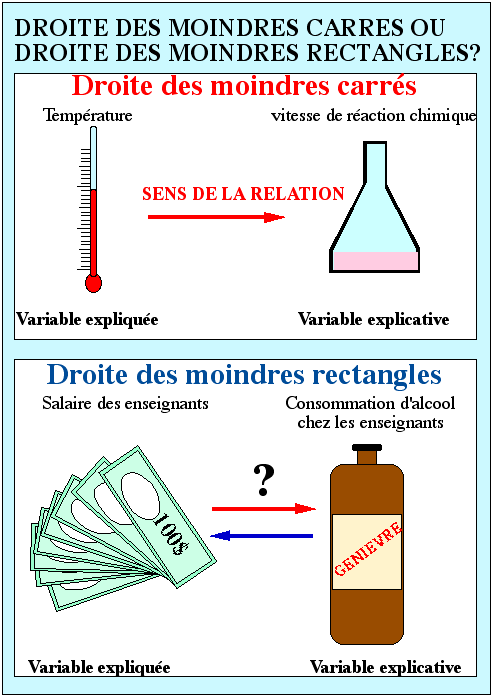
Â
Â
Interpolation et extrapolation:
L'équation de la droite de régression permet d'estimer une valeur de x connaissant un y déterminé ou une valeur de y pour un x déterminé.
Une
interpolation permet d'estimer une valeur tout en restant dans les limites de valeurs de l'échantillon.Si la valeur à évaluer se trouve en dehors des limites de l'échantillon, on parlera d'
extrapolation. Dans ce cas, il faut rester prudent: si les valeurs s'éloignent trop des limites de l'échantillon, le modèle risque de ne plus être linéaire et l'extrapolation sera aberrante. Par exemple: quelle serait l'envergure d'une chauve-souris de 53 grammes? Selon le modèle linéaire, nous pourrions croire que l'envergure correspondante devrait être de 480 mm alors que la relation réelle tend à s'infléchir (envergure réelle: 450 mm).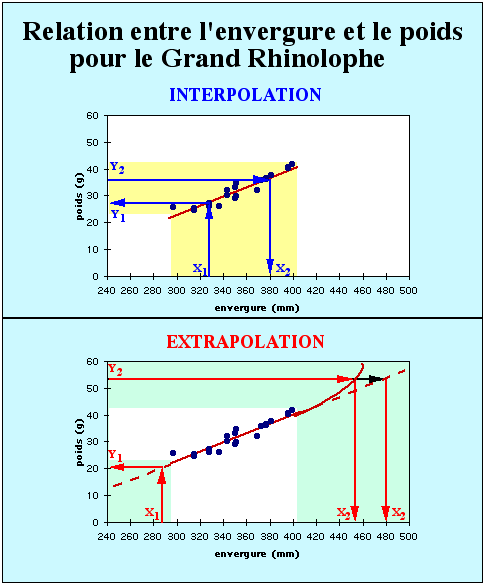
Â
Â
TRANSFORMATION DE VARIABLES.
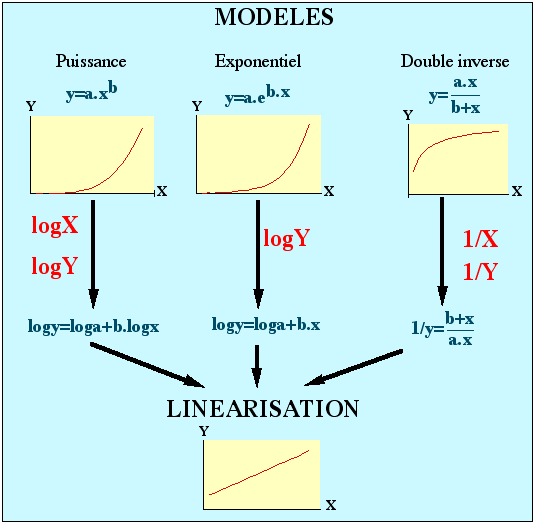
Â
Â