introduction

standard

indépendants

appariés

formulaire

décision

Tests d'hypothèses:

Les tests d'hypothèses vont permettre aux statisticiens de comparer des échantillons entre eux ou encore de comparer un échantillon avec une population de référence...

Type de test d'hypothèses:

Dans le cadre de ces travaux pratiques, nous envisagerons trois types de tests d'hypothèses.

1. test de comparaison d'une moyenne d'un échantillon par rapport à une population
2. test de comparaison de 2 échantillons tirés de 2 populations indépendantes
3. test de comparaison de 2 échantillons tirés de 2 populations pairées

Les hypothèses:

Quelque soit le type de tests (voir ci-dessus), il faut toujours considérer a priori que la (les) moyenne(s) comparées proviennent de une seule population de moyenne Mx. Il s'agit de l'hypothèse de départ appelée "hypothèse nulle" (H0) qui pourra s'écrire comme suit:

L'expérimentateur doit démontrer que la (les) moyenne(s) ne provien(nen)t pas de la même population, mais qu'une des population possède une moyenne plus grande, plus petite ou tout simplement différente par rapport à l'autre population. Il s'agit de l'"hypothèse alternatique" (H1) qui pourra s'écrire comme suit:

ou encore

ou encore

Réalisation du test:

Réduction des moyennes observées:

La (les) moyenne(s) mx obtenue(s) pour (les) l'échantillon(s) peu(ven)t être réduite(s) en une valeur observée (z observée ou t observée). Celle-ci peut ensuite être comparée à une valeur seuil (z table ou t table).

Recherche d'une limite arbitraire, une valeur seuil:

La valeur seuil va déterminer sous la courbe de Gauss réduite des zones distinctes: une zone répondant aux exigences de l'hypothèse nulle H0 et une zone répondant aux exigences de l'hypothèse alternative H1. En fonction H1et de l'erreur de type I que vous souhaitez accorder au test (alpha = 5% ou 1% ou 0,1%), vous devrez choisir dans les tables de Z ou de T de student une valeur seuil.

Comparer la valeur réduite observée à la valeur seuil trouvée dans les tables:

Si l'hypothèse alternative H1 est "M1 plus grand que M2"

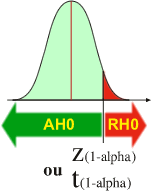Lorsque la valeur observée (Z observée ou t observée) est plus grande que la valeur théorique (Z(1-alpha) ou t(1-alpha)), alors H1 est respectée (AH1)et H0 rejetée (RH0). Dans le cas d'un rejet de H0 (RH0), l'expérimentateur aura réussi a démontrer que les moyennes comparées sont telles que M1 est plus grande que M2. Comme la valeur de alpha choisie par l'expérimentateur est très faible (maximum 5%), un RH0 signifie que la distance qui sépare les moyennes comparées est trop élévée que pour être simplement dûe au hasard. Le risque de se tromper lorsque RH0 est donc très faible. Un RH0 permet à l'expérimentateur d'être quasiment certain que M1 est bien plus grand que M2 avec un risque de se tromper équivalent à alpha. Dans le cas d'une acceptation de H0 (AH0), l'expérimentateur est obligé de considérer que les moyennes comparées sont identiques. Cette AH0 doit être considérée par l'expérimentateur comme une "mise en échec". A la différence de la "quasi certitude" au sujet de la conclusion tirée quand RH0, dans le cas d'une AH0, rien ne permet à l'expérimentateur d'être certain que les moyennes comparées sont effectivement identiques.

Si l'hypothèse alternative H1 est "M1 plus petit que M2"

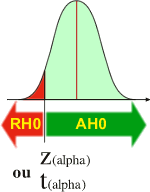Lorsque la valeur observée (Z observée ou t observée) est plus petite que la valeur théorique (Z(alpha) ou t(alpha)), alors H1 est respectée (AH1)et H0 rejetée (RH0). Dans le cas d'un rejet de H0 (RH0), l'expérimentateur a la "quasi certitude" que M1 est plus petit que M2 avec une probabilité de se tromper de alpha (maximum 5%). Dans le cas d'une acceptation de H0 (AH0), l'expérimentateur n'a pas réussi à démontrer que M1est plus petite que M2. Le doute est toujours possible.

Si l'hypothèse alternative H1 est "M1 différent de M2"

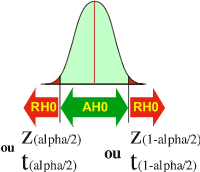Lorsque la valeur observée (Z observée ou t observée) est SOIT plus petite que la valeur théorique (Z(alpha/2) ou t(alpha/2)), SOIT plus grande que la valeur théorique (Z(1-alpha/2) ou t(1-alpha/2)), alors H1 est respectée (AH1)et H0 rejetée (RH0). Dans le cas d'un rejet de H0 (RH0), l'expérimentateur a la "quasi certitude" que M1 différent de M2 avec une probabilité de se tromper de alpha (maximum 5%). Dans le cas d'une acceptation de H0 (AH0), l'expérimentateur n'a pas réussi à démontrer que M1est différent de M2. Le doute est toujours possible.