Test de comparaison d'un moyenne d'un échantillon par rapport à une population standard |

Principe:
Un échantillon d'individus est prélevé et sa moyenne est calculée (mx). Cet échantillon provient-il d'une population 1 déterminée de moyenne M1 (ou µ1) ou bien appartient-il à une seconde population appelée population 2 de moyenne M2? Autrement dit, cet échantillon est-il conforme à la population d'origine?
les hypothèses:
Hypothèse nulle H0:
| H0: M1 = M2 = Mx |
la moyenne de l'échantillon appartient
à la population de référence de moyenne M1
|
Hypothèse alternative H1:
| H1: M1 plus grand que M2 . |
la moyenne de l'échantillon appartient
à une population dont la moyenne M2 est supérieure
à la moyenne M1 de la population de référence
|
ou encore
| H1: M1 plus petit que M2 . |
la moyenne de l'échantillon appartient
à une population dont la moyenne M2 est inférieure
à la moyenne M1 de la population de référence
|
ou encore
| H1: M1 différent de M2 . |
la moyenne de l'échantillon appartient
à une population dont la moyenne M2 est différente
de la moyenne M1 de la population de référence
|
Calculer la valeur observée:
Cas 1: la variance de la population de référence est connue:
La réduction de ma moyenne de l'échantillon peut se faire par le cacul d'une valeur de Z observé dont la formule est la suivante:
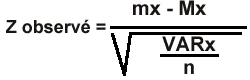
Où mx est la moyenne de l'échantillon; Mx est la moyenne de la population de référence; VARx est la variance de la population de référence; n est la taille de l'échantillon.
Trouvez dans les tables de Z, la ou les valeurs seuil en tenant compte de alpha et de H1.
|
AH0 (et donc RH1)
|
L'échantillon de moyenne mx appartient à la population de référence dont la moyenne est M1 |
|
RH0 (et donc AH1)
|
L'échantillon de moyenne mx n'appartient pas à la population de référence dont la moyenne est M1mais à une population dont la moyenne M2 est plus grande OU plus petite OU différente par rapport à la population de référence dont la moyenne est M1. |
Cas 2: la variance de la population de référence est inconnue:
Dans ce cas, il n'est plus possible de calculer directement une valeur de z observée car il nous manque la valeur de la variance de la population de référnce VARx.
Cependant, il est toujours posible d'adapter cette formule en remplacant VARx par une approximation de celle-ci. Cette approximation est donnée par l'estimateur de la variance de la population varx. La variable réduite ainsi obtenue n'est plus une variable z observée mais une variable t observée.
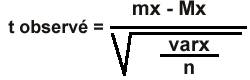
Où mx est la moyenne de l'échantillon; Mx est la moyenne de la population de référence; varx est l'estimateur de la variance de la population (autrement dit la SCE/(n-1) qui est une valeur propre a l'échantillon); n est la taille de l'échantillon.
Ensuite, il reste à trouver dans les tables de t de Student (l'aspect de la courbe est aussi une courbe de Gauss), la ou les valeurs seuil en tenant compte de alpha et de H1. La valeur de t de Student nécessite aussi la détermination d'un certain nombre de degrés de liberté. Pour trouver la ou les valeurs seuil, il fat donc rechercher:
tseuil;(n-1) degrés de liberté
Où "seuil" représente H1 (seuil peut être (1-alpha) ou alpha ou (1-alpha/2) ou (alpha/2); n est la taille de l'échantillon
|
AH0 (et donc RH1)
|
L'échantillon de moyenne mx appartient à la population de référence dont la moyenne est M1 |
|
RH0 (et donc AH1)
|
L'échantillon de moyenne mx n'appartient pas à la population de référence dont la moyenne est M1mais à une population dont la moyenne M2 est plus grande OU plus petite OU différente par rapport à la population de référence dont la moyenne est M1. |