Test de comparaison de deux moyennes (observations pairées) |

Principe:
Un expérimentateur dispose d'uné série d'observations associées par paires ou par couples. Par exemple, une expérience à été menée sur des rats. Ils ont été pesés avant et après un traitement hautement énergétique. A chaque individu de l'expérience est associé une pesée avant et après le traitement.
Pour traiter ce genre de test, l'expérimentateur doit considérer la différence de chaque couple de données. Toutes ces différences forment un échantillon dont on peut calculer la moyenne mD et la variance varD.
L'expérimentateur doit ensuite comparer la moyenne mD des échantillons pairés avec la moyenne des différences attendues MD.
Son point de départ est de considérer que la moyenne de différences mD de sont échantillon provient d'une population de différences de moyenne MD égale à delta (exemple: le traitement hautement énergétique ne provoque aucune modification de poids chez les rats, doù delta vaut 0). L'expérimentateur a pour objectif de montrer que la moyenne des différences mD provient d'une population de moyennes de différences MD est différente de delta (exemple: le traitement hautement énergétique provoque une modification de poids chez les rats, d'où delta devrait être plus grand que 0).
les hypothèses:
Hypothèse nulle H0:
| H0: MD = delta |
la moyenne des différences de la population
de référence est nulle
|
Hypothèse alternative H1:
| H1: MD est différente de delta |
la moyenne des différences de la population
de référence est non nulle
|
Calculer la valeur observée:
La réduction de la moyenne des différences peut se faire par le cacul d'une valeur de t observé dont la formule est la suivante:
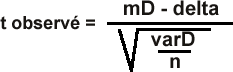
Où mD est la moyenne des différences des données pairées; varD est la variance des différences des données pairées; n est le nombre de couples de données.
Trouvez dans les tables de t, la ou les valeurs seuil en tenant compte de alpha pour un test bidirectionnel. Le nombre de degré de liberté a employer est (n-1) dl où n est le nombre de couples de données.
t tables, (n-1) dl; (1-alpha/2)
|
AH0 (et donc RH1)
|
la moyenne des différences de la population de référence est nulle |
|
RH0 (et donc AH1)
|
la moyenne des différences de la population de référence est non nulle |