Formulaire relatif aux tests d'hypothèses
Comparer une moyenne à un standard:
|
H0: M1 = M2 = Mx
|
||
| ou bien |
1
|
H1: M1 plus grand que M2 .
|
|
2
|
H1: M1 plus petit que M2 .
|
|
|
3
|
H1: M1 différent de M2 .
|
|
|
Si la
variance de la population standard (VARx) est connue
|
Si la
variance de la population standard (VARx) est inconnue
|
||
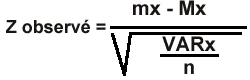 |
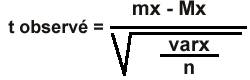 |
||
|
1
|
Z tables; (1-alpha)
|
1
|
t tables; (n-1) dl; (1-alpha)
|
|
2
|
Z tables; (alpha)
|
2
|
t tables; (n-1) dl; (alpha)
|
|
3
|
Z tables; (alpha/2) Z tables;(1-alpha/2) |
3
|
t tables; (n-1) dl; (alpha/2) t tables;(n-1) dl; (1-alpha/2) |
Test de comparaison d'un moyenne d'un échantillon par rapport à une population standard:
|
H0: M1 = M2 = Mx
|
||
| ou bien |
1
|
H1: M1 plus grand que M2 .
|
|
2
|
H1: M1 plus petit que M2 .
|
|
|
3
|
H1: M1 différent de M2 .
|
|
|
Si les
variances des populations (VAR1 et 1) sont connues
|
Si
les variances des populations (VAR1 et 1) sont
inconnues
|
||
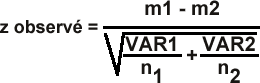 |
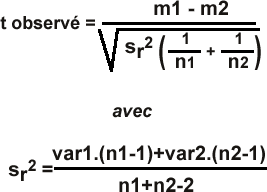 |
||
|
1
|
Z tables; (1-alpha)
|
1
|
t tables; (n1+n2-2) dl; (1-alpha)
|
|
2
|
Z tables; (alpha)
|
2
|
t tables; (n1+n2-2) dl; (alpha)
|
|
3
|
Z tables; (alpha/2) Z tables;(1-alpha/2) |
3
|
t tables; (n1+n2-2) dl; (alpha/2) t tables;(n1+n2-2) dl; (1-alpha/2) |
Comparer deux moyennes (observations pairées)
| H0: MD = delta |
la moyenne des différences de la population
de référence est nulle
|
| H1: MD est différente de delta |
la moyenne des différences de la population
de référence est non nulle
|
|
La variance
de la population (VARD) est toujours inconnue
|
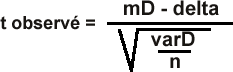 |
|
t tables, (n-1) dl; (1-alpha/2)
avec n nombre de couples
|