Corrig� |
salaire |
ni |
ai |
ui |
di = ni/ui | Ni |
Fi |
Ci |
ni Ci |
[50,60[ |
20 |
10 |
1 |
20 |
0 |
0 |
55 |
1100 |
[60,70[ |
60 |
10 |
1 |
60 |
20 |
0,1 |
65 |
3900 |
[70,90[ |
50 |
20 |
2 |
25 |
80 |
0,4 |
80 |
4000 |
[90,100[ |
40 |
10 |
1 |
40 |
130 |
0,65 |
95 |
3800 |
[100,130[ |
30 |
30 |
3 |
10 |
170 |
0,85 |
115 |
3450 |
200 |
1 |
16250 |
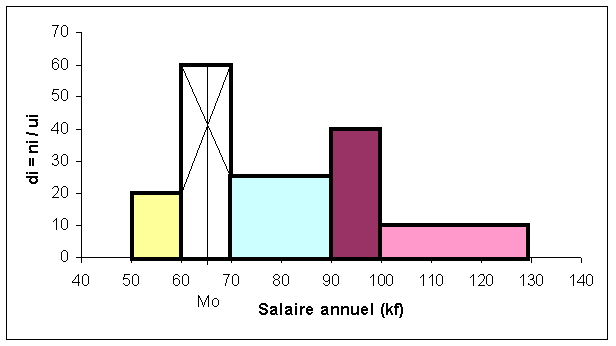
1. Histogramme : Les classes de valeur de la variable sont d’amplitude in�gale. On prendra comme " unit� " d’amplitude u = 10.

2. La classe modale est la classe [60, 70[. Pour avoir une valeur unique, il est possible de retenir le centre de la classe modale, ici 65 ou bien d’appliquer la m�thode des diagonales, dans ce cas on peut estimer graphiquement le mode � 65,5.
Le calcul du mode par la m�thode des diagonales donne :
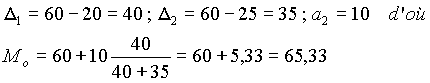
3. Le salaire m�dian :
La classe m�diane est la classe [70, 90[. Effectuons un calcul d’interpolation lin�aire :
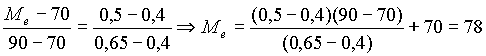
4. Le salaire moyen a pour valeur :
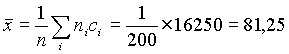
5. La position respective des trois caract�ristiques est la suivante :
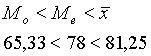
On peut en d�duire que la distribution est �tal�e vers la droite.
6. La relation empirique de Pearson est la suivante :
1 (mode) + 2 (moyenne) = 3 (m�diane)
calcul de la moyenne � partir des deux autres caract�ristiques :
65,33 + 2(moyenne) = 3(78) d’o�
moyenne = (234 – 65,33)/2 = 84,33
La diff�rence que l’on constate entre la valeur estim�e de la moyenne par la relation de Pearson et la valeur calcul�e � la question 4) provient de l’asym�trie de la distribution. En effet la relation de Pearson n’est relativement bien v�rifi�e que dans le cas de distributions faiblement asym�triques.