Approximation binomiale de la distribution normale
Cette page calcule le rapport z binomial pour les situations du type k évenements parmi n avec la formule
|
| z =
| (k—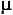 )±.5 )±.5
-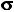
|
où :
-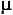 = np = np
| [moyenne de la distribution d'échantillonnage binomiale]
-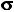 = racine carré de[npq] = racine carré de[npq]
| [l'écart-type (déviation standard) de la distribution d'échantillonnage binomiale]
| |
|
| n =
| Nombre d'expériences permettant d'obtenir l'évenement x ou nombre total d'expériences ;
| k =
| Nombre de réalisations observées ou attendues de l'évenement x ;
| p =
| Probabilité de l'événement x à chaque expérience; et
| q =
| Probabilité que l'événement x ne se réalise pas à chaque expérience.
| | | |
Par exemple : Lors de 20 jets indépendants d'une même pièce de monnaie, quelle est la probabilité d'obtenir autant que 16 faces sur les 20 jets (i.e., 16 faces ou plus sur 20 lancers)?
Dans ce cas
|
| n = 20
| [possibilités d'obtenir une face]
| k = 16
| [le nombre attendu de faces]
| p = 0,5
| [la probabilité d'obtenir une face à chaque lancer]
| q = 0,5
| [la probabilité de ne pas obtenir une face à chaque lancer]
| | | |
Alternativement : lors de 20 lancers d'une pièce, quelle est la probabilité d'obtenir aussi peu que 8 faces sur 20 lancers (i.e., 8 faces ou moins sur 20 lancers)? Dans ce cas, n = 20, k = 8, p = 0,5, et q = 0,5.
Pour réaliser ce calcul, saisir les valeurs appropriées de n, k, et p (la valeur de q est calculée et affichée automatiquement). Ensuite, appuyez sur le bouton "Calcul".
Pour saisir un nouvel ensemble de valeurs n, k, et p, appuyez sur le bouton "Remise à zéro". La valeur de p peut être saisie soit comme fraction décimale telle que 0,25 ou comme fraction ordinaire telle que 1/4. Il est prérérable de saisir les fractions ordinaires plutôt que les fractions décimales arrondies : 1/3 plutôt que 0,3333; 1/6 plutôt que 0,1667.
La langage de programmation JavaScript utilisé pour effectuer les calculs, implique l'emploi du point au lieu de la virgule. Par exemple, saisir 0.5 au lieu de 0,5.
Les probabilités unilatérale et bilatérale associées à la valeur de z sont calculées.
Attention, cette analyse n'est valide que si np et nq sont tous les deux égaux ou supérieurs à 5.
Si cette condition n'est pas satisfaite, utilisez le calculateur de probabilité binomial exacte, si n est égal ou inférieur à 170.
Si n>170, utilisez l'approximation de Poisson des probabilités binomiales.
Modifié d'après Richard Lowry 1998-2000