


Introduction aux Statistiques
Citation :
Introduction aux statistiques - © 1996, Ramousse R., Le Berre M. & Le Guelte L.
   |
|
L'ajustement linéaire est une technique analogue à l'analyse factorielle, mais beaucoup plus simple.
Prenons l'exemple suivant : considérons le nuage de points associé au tableau des mesures de pH et de conductivité d'une rivière, en 4 points différents, et lors de mesures aux quatre saisons (ce sont les 2 premières colonnes du tableau ci-dessous).
| Station |
|
|
|
|
|
|
|
|
|
|
| 1p |
|
|
|
|
|
|
|
|
|
|
| 1e |
|
|
|
|
|
|
|
|
|
|
| 1a |
|
|
|
|
|
|
|
|
|
|
| 1h |
|
|
|
|
|
|
|
|
|
|
| 2 p |
|
|
|
|
|
|
|
|
|
|
| 2 e |
|
|
|
|
|
|
|
|
|
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
| 2 h |
|
|
|
|
|
|
|
|
|
|
| 3 p |
|
|
|
|
|
|
|
|
|
|
| 3 e |
|
|
|
|
|
|
|
|
|
|
| 3 a |
|
|
|
|
|
|
|
|
|
|
| 3 h |
|
|
|
|
|
|
|
|
|
|
| 4 p |
|
|
|
|
|
|
|
|
|
|
| 4 e |
|
|
|
|
|
|
|
|
|
|
| 4 a |
|
|
|
|
|
|
|
|
|
|
| 4 h |
|
|
|
|
|
|
|
|
|
|
On veut avoir une idée des interrelations entre les 10 variables. Les méthodes d’analyse factorielles consistent à déterminer de nouvelles variables, les facteurs, qui résument au mieux les 10 variables initiales.
Chaque facteur est une combinaison linéaire des variables initiales :
F1 = a1X1+ ... + a10X10
Deux facteurs engendrent un plan factoriel. Si l’on veut, par exemple, représenter les données dans un plan, on cherchera à ce que, sur ce plan, les "distances"entre les stations soient les plus proche possibles des distances initialement calculées.
Si l’on effectue la représentation de ces mesures dans un graphique plan, on obtient un nuage de points dans un espace à 2 dimensions.
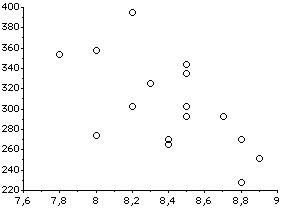
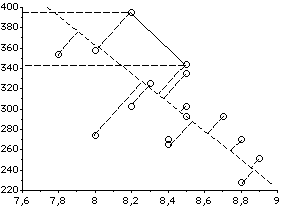
Le nuage de points présente une forme allongée. Ces points sont au voisinage d'une droite D. Le problème est donc de déterminer la droite D à partir des mesures effectuées. Cette droite doit ajuster au mieux le nuage des points expérimentaux. Depuis longtemps, la technique utilisée est celle dite des moindres carrés qui permet de réaliser par le calcul le choix optimum de la droite (d'où le nom d'ajustement linéaire).
Pour passer à l'objet de l'analyse factorielle, il faut modifier sur plusieurs points le modèle de l'ajustement linéaire tout en imaginant qu'au lieu d'étudier la relation entre 2 variables, on décide d'étudier la relation entre plusieurs variables. Supposons donc qu'au lieu de mesurer deux grandeurs, on en mesure un plus grand nombre.
Soit, par exemple, l'étude des variations de 10 variables le long de la même rivière : A chaque ligne, on associe ses mesures de qualité sous différents aspects : X1 (pH), X2 (conductivité), X3 (oxygène), X4 (DBO5 : demande biologique en oxygène), X5 (oxydabilité). X6 (N4 : ammoniaque), X7 (N3 : nitrates), X8 (P4 : phosphates), X9 (TE : température) et X10 (DE : débit).
Analyser toutes les variables [X1, X2, . . . X10] prises deux à deux ne permet pas la synthèse. Ainsi, au lieu de savoir si une variable Xi est liée à une autre Xj pour chacun des couples de variables (Xi, Xj), on veut savoir comment varient simultanément toutes les variables (X1, X2, ..., X10).
On peut résumer l'information par un plus petit nombre de variables :
Point-ligne i = ai F + bi F2
On va chercher un premier plan factoriel qui représente au mieux le nuage des points-lignes originellement représenté dans un espace à 10 dimensions.
Pour montrer ce que sont les facteurs, et pour simplifier, prenons l'exemple où nous ne mesurons que trois grandeurs X1, X2, X3 qu'on peut représenter dans l'espace à trois dimensions.
Chaque point-ligne du nuage a, sur les axes X1, X2, X3, trois projections situées à des distances de O égales à ses valeurs dans les variables X1, X2, X3.
Le centre de gravité G est un point-ligne fictif qui a pour coordonnées la moyenne des valeurs dans chacune des variables. Autour de ce centre, le nuage peut présenter différents aspects :
• Il peut apparaître sphérique ; dans ce cas, il n'y a pas de facteur privilégié.
• Il se peut, au contraire, que le nuage soit allongé, le long de la droite passant par le centre : cette droite est un axe factoriel. On peut graduer cette droite à partir du point G. C'est à partir de cette graduation qu'on mesurera la valeur du facteur pour un point-région donné. On notera les angles faits par les axes factoriels F1, F2, F3 et les axes OX1, OX2, OX3 ; si F est perpendiculaire à OX1, alors X1 varie peu et X1 n'intervient que faiblement dans le calcul du facteur F ; si F fait un angle faible avec OX1, c'est au contraire que X1 varie beaucoup et que X1 intervient beaucoup dans le calcul du facteur F.
• S'il n'y avait aucune liaison entre les variables, le nuage aurait une forme sans structure.
Ici, pour l'ensemble de la population, le nuage de points a une forme ovale. Pour étudier la structure de ce nuage, on le réduit de plusieurs points de vue :
• On recherche la tendance centrale, en prenant la moyenne de tous les pH et la moyenne de toutes les conductivités. On obtient un individu hypothétique G situé au centre de gravité du nuage. Cet individu est fictif et ne correspond pas à un individu réel de la population.
• On recherche les principales manières dont les individus s'écartent de la moyenne : on observe les tendances de dispersion autour du centre de gravité. Ici, il y a deux directions qui indiquent la dispersion : un axe de plus grand allongement F1 et un axe de plus petit allongement F2.
Pour le même nuage, nous avons deux systèmes de repérage : le système des axes initiaux et le système (F1, F2) des axes principaux d'inertie. Il en résulte donc un changement d'axes.
On part de la remarque suivante. Dans le système initial, les points-lignes 1 et 2 sont figurés par les points A et B. Dans le même système à un seul axe F1, les points-lignes 1 et 2 sont figurés par leurs projections C et D.
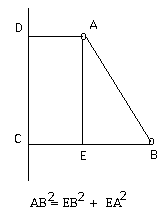
Alors que les points A et B étaient distants de d (=AB) dans l'espace initial, ils sont distants de h (CD=EA) dans l'espace réduit au facteur F1.
Si on voulait réduire la représentation à F1 seul, on aurait une perte d'information au sens où, au lieu d'avoir : distance (AB) = d (distance réelle), on a maintenant : distance (CD) = h (distance projetée).
Une des manières de mesurer la perte d'information dans le passage du premier système au second est de regarder la figure où se trouvent d (AB) et h (CD).
On a : d2 = h2 + e2 (théorème de Pythagore)
Soit : e2 = d2 - h2 ; e2 est donc une mesure de l'écart entre la réalité et son approximation h sur F1. Si l’on veut la meilleure approximation possible, il faut que l'ensemble des écarts soit tel que e soit le plus petit possible. S’il n'y avait que deux points-lignes 1 et 2, la meilleure solution serait de rendre la quantité e nulle. C'est-à-dire, de faire passer F1 par 1 et 2, ou de rendre F1 parallèle à 1 - 2. Il n'y aurait aucune distorsion :
d2 = h2 +e2 avec e2 = 0
Mais il n'y a pas que deux points-lignes, mais 16 dans notre exemple. On considère donc que le meilleur choix pour F1 est celui pour lequel la somme des e2 pour toutes les lignes est minimale. F1 est la droite des moindres carrés.
Minimiser e2, c'est aussi maximiser h2 : d2 = h2 + e2.
L'ensemble des h2 s'appelle inertie sur F1 du nuage de points. On dira que F1 est la droite qui extrait le maximum d'inertie du nuage. F1 s'appelle un axe factoriel (ou facteur). C'est le premier axe factoriel.
En écrivant autrement les formules, on pourrait montrer que F1 maximise aussi la variance extraite. Il y a donc, à première lecture, une équivalence entre les termes (variance, inertie) apportée par l'ensemble des points du nuage.
Pour choisir le second axe factoriel F2, on impose deux contraintes :
• Entre l'inertie globale et celle du F1, il y a une inertie résiduelle ; F2 est celle des droites qui extrait le plus possible de cette inertie résiduelle. Mais si on limitait là la contrainte, F2 serait indéterminé. On ajoute une seconde contrainte ;
• F2 est orthogonal à F1.
L'extraction de F1 (premier axe principal d'inertie du nuage) est fondée sur un critère global. C'est globalement que F1 respecte le jeu des distances entre points-lignes. Il se peut que, localement, le critère ne soit pas respecté, d'où la nécessité de se protéger des erreurs de perspective. Ce sera un des rôles de certains indicateurs appelés "aides à l'interprétation".
Les résultats d'une analyse factorielle ne méritent pas toujours d'être publiés. Ils le seront chaque fois qu'ils remplissent une fonction iconographique (illustration de tableaux de contingence par exemple). Leur rôle est alors de rendre plus facile la lecture de ces tableaux. La partie publiable des résultats ne représente en général qu'une petite fraction des calculs effectués.
Les rubriques suivantes doivent nécessairement accompagner chaque analyse.
1) Dimension du tableau
Nombres de variables et d'individus dans le cas d'une analyse en composantes principales, nombres de lignes et de colonnes dans le cas de l'analyse des correspondances d'une table de contingence.
2) Nature et codage du tableau
S'agit-il de mesures numériques continues, de codage de présence-absence. S'agit-il d'effectifs, de pourcentages ?
3) Liste des variables
ll est important d'avoir une idée du caractère représentatif des variables destinées à être synthétisée. ll n'est pas possible de juger de la pertinence d'un facteur sans connaître cette liste.
4) Valeurs propres et taux d’inertie
Liste (ou indication sur le graphique) des valeurs propres et des taux d'inertie (ou encore : pourcentages de variance expliquée). En général, on se fixe comme limite d'arrêt l'atteinte de 80 % de la variance (en sommant la variance des facteurs F1, F2, F3, ...).
5) Aides à l'interprétation
Ce sont les contributions absolues et relatives. II n'est pas indispensable de publier la liste exhaustive de ces paramètres. Elle est en général encombrante. Les contributions absolues supérieures à la moyenne (obtenues en divisant 1000 par le nombre d'éléments (nombre d'éléments -1 pour une AFC)) qui indiquent comment une variable participe à la construction d'un axe, pourront être citées pour étayer l'éventuelle caractérisation de l'axe. Les contributions absolues trop fortes (de l'ordre de 40 à 50 % par exemple) sont en général suspectes : elles traduisent un certain déséquilibre de la synthèse. Si les axes se réduisent en effet à certains composants élémentaires, cela signifie que le seul fait mis en évidence est l'hétérogénéité du tableau.
Les contributions relatives peuvent être fortes : elle traduisent dans ce cas la caractérisation exclusive de l'axe par une ou quelques variables. On se fixera comme limite inférieure 0,5 (ou 500 selon l'expression des valeurs sur le listage) en général, puisque les contributions relatives s'assimilent à des carrés de coefficient de corrélation soit ici 0,7*0,7 = 0,49 = 0,5).
Un axe "significatif" du point de vue statistique n'a pas nécessairement une interprétation : on peut au contraire trouver une interprétation à une direction diagonale ou à de simples regroupements dont les axes eux-mêmes rendent mal compte.
6) Aménagements graphiques
On peut clarifier la lecture des plans factoriels en joignant par des contours les modalités ordonnées de façon naturelle (classes de revenu, âge, nombre d'enfants, tailles, etc.). On allègera le graphique en éliminant les variables dont la position n'est pas "significative" (en général celles situées près de l'origine des axes).