


Introduction aux Statistiques
Citation :
Introduction aux statistiques - ﺡ۸ 1996, Ramousse R., Le Berre M. & Le Guelte L.
   |
|
7. Corrﺣ۸lation : Mesure et test de signification
Il faut distinguer deux situations :
• une des deux variables, la variable dﺣ۸pendante, doit ﺣ۹tre exprimﺣ۸e en fonction de l’autre, la variable indﺣ۸pendante, de faﺣ۶on ﺣ prﺣ۸voir ou estimer l’une en fonction de l’autre. Les valeurs de la variable indﺣ۸pendante sont fixﺣ۸es par avance par l’expﺣ۸rimentateur.
Exemples :• Les deux variables ne peuvent ﺣ۹tre distinguﺣ۸es, et pourront prendre n’importe quelle valeur pour n’importe quel individu observﺣ۸. Les variables sont dites interdﺣ۸pendantes.
Exemple :ﺡ
7.1. Le coefficient de contingenceMﺣ۸thode
| ﺡ |
A1 |
A2 |
... |
Ac |
Total |
|
B1 |
(A1B1) |
(A2B1) |
.... |
AcB1 |
ﺡ |
|
B2 |
(A1B2) |
(A2B2) |
.... |
AcB2 |
ﺡ |
|
- |
ﺡ | ﺡ | ﺡ | ﺡ | ﺡ |
|
Br |
(A1Br) |
(A2Br) |
.... |
(AcBr) |
ﺡ |
|
Total |
ﺡ | ﺡ | ﺡ | ﺡ |
N |
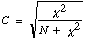 | et | 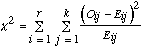 |
oﺣﺗ
Exemple
| Filiﺣ۷re | I et II | III | IV | V | Total |
| Prﺣ۸pa U. | 7,3 23 | 30,3 40 | 38,0 16 | 5,4 2 | 81 |
|---|---|---|---|---|---|
| Gﺣ۸nﺣ۸ral | 18,6 11 | 77,5 75 | 97,1 107 | 13,8 14 | 207 |
| Commercial | 9,1 1 | 38,2 31 | 47,9 60 | 6,8 10 | 102 |
| Total | 35 | 146 | 183 | 26 | 390 |
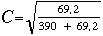 | = 0,39. |
Test de la signification du coefficient de contingence
Limitations du coefficient de contingence
ﺡ
7.2. Coefficient de corrﺣ۸lation de rang de KendallPrincipe et mﺣ۸thode
|
Dissertation |
a |
b |
c |
d |
|
Enseignant A |
3 |
4 |
2 |
1 |
|
Enseignant B |
3 |
1 |
4 |
2 |
|
Dissertation |
d |
c |
a |
b |
|
Enseignant A |
1 |
2 |
3 |
4 |
|
Enseignant B |
2 |
4 |
3 |
1 |
| (A) |
oﺣﺗ N = le nombre d'objets ou d'individus rangﺣ۸s dans les deux sﺣ۸ries.
- 0,33 |
Exemple
La relation entre l'autoritarisme des ﺣ۸tudiants et leur conformisme social est recherchﺣ۸. L'autoritarisme des sujets et leur conformisme social sont apprﺣ۸ciﺣ۸s par le passage de tests. Les rﺣ۸sultats obtenus ﺣ ces deux tests par chacun de 12 ﺣ۸tudiants et leurs rangs (en italique) sont prﺣ۸sentﺣ۸s dans le tableau suivant :
| Etudiant | Apprﺣ۸ciations | |||
| de l'autoritarisme | du conformisme | |||
| A | 82 | 2 | 42 | 3 |
|---|---|---|---|---|
| B | 98 | 6 | 46 | 4 |
| C | 87 | 5 | 39 | 2 |
| D | 40 | 1 | 37 | 1 |
| E | 116 | 10 | 65 | 8 |
| F | 113 | 9 | 88 | 11 |
| G | 111 | 8 | 86 | 10 |
| H | 83 | 3 | 56 | 6 |
| I | 85 | 4 | 62 | 7 |
| J | 126 | 12 | 92 | 12 |
| K | 106 | 7 | 54 | 5 |
| L | 117 | 11 | 81 | 9 |
ﺡ
|
Sujet |
D |
C |
A |
B |
K |
H |
I |
E |
L |
G |
F |
J |
| ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ | ﺡ |
|
Conformisme social |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Autoritarisme |
1 |
5 |
2 |
6 |
7 |
3 |
4 |
10 |
11 |
8 |
9 |
12 |
0,67 |
qui reprﺣ۸sente le degrﺣ۸ de relation entre l'autoritarisme et le conformisme social de 12 ﺣ۸tudiants.
Observations ex-ﺣ۵quo
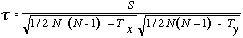 | (A’) |
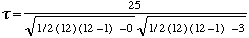 | = 0,39 |
Test de signification de
et un ﺣ۸cart-type | 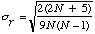 . . | Alors | 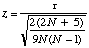 |
Exemple pour un ﺣ۸chantillon de taille supﺣ۸rieure ﺣ 10
| Nous pouvons calculer | 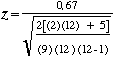 | = 3,03 |
Exercice :
| 1er expert | 2ﺣ۷me expert |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculer le coefficient de corrﺣ۸lation, et concluez.
ﺡ
7.3. Coefficient de corrﺣ۸lation de rang partiel de Kendall
Principe
| Sujet |
a |
b |
c |
d |
|
rangs de Z |
1 | 2 | 3 | 4 |
|
rangs de X |
3 | 1 | 2 | 4 |
|
rangs de Y |
2 | 1 | 3 | 4 |
|
Paire |
(a,b) |
(a,c) |
(a,d) |
(b,c) |
(b,d) |
(c,d) |
|
Z |
+ | + | + | + | + | + |
|
X |
- | - | + | + | + | + |
|
Y |
- | + | + | + | + | + |
| Paires de Y dont le signe concorde avec celui de Z | Paires de Y dont le signe ne concorde pas avec celui de Z | Total | |
| Paires de X dont le signe concorde avec celui de Z | A 4 | B 0 | 4 |
|---|---|---|---|
| Paires de X dont le signe ne concorde pas avec celui de Z | C 1 | D 1 | 2 |
| Total | A+C 5 | B+D 1 | 6 |
| (B) |
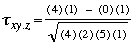 | = 0,63 |
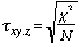
Mﺣ۸thode
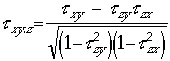 | (C) |
Exemple
ﺡ
| ﺡ |
Rangs |
||
|
Sujet |
Conformisme |
Autoritarisme |
Conformitﺣ۸ |
| ﺡ |
X |
Y |
Z |
|
A |
3 |
2 |
1,5 |
|
B |
4 |
6 |
1,5 |
|
C |
2 |
5 |
3,5 |
|
D |
1 |
1 |
3,5 |
|
E |
8 |
10 |
5,0 |
|
F |
11 |
9 |
6,0 |
|
G |
10 |
9 |
7,0 |
|
H |
6 |
3 |
8,0 |
|
I |
7 |
4 |
9,0 |
|
J |
12 |
12 |
10,5 |
|
K |
5 |
7 |
10,5 |
|
L |
9 |
11 |
12,0 |
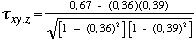 | = 0,62 |
Test de signification
ﺡ
ﺡ
ﺡ
7.4. Coefficient de concordance de Kendall W (Kendall coefficient of concordance)
Principe
| Postulant | ||||||
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| Cadre A | 1 | 6 | 3 | 2 | 5 | 4 |
| Cadre B | 1 | 5 | 6 | 4 | 2 | 3 |
| Cadre C | 6 | 3 | 2 | 5 | 4 | 1 |
| Rj | 8 | 14 | 11 | 11 | 11 | 8 |
Mﺣ۸thode
oﺣﺗ s = somme des carrﺣ۸s des dﺣ۸viations entre les Rj observﺣ۸s et la moyenne de ces Rj.
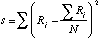
k = nombre de sﺣ۸ries de rangements, nombre de juges.
N = nombre d'individus rangﺣ۸s
1/12 k2 (N3 - N) = la somme s que l'on obtiendrait dans le cas d'un accord parfait entre les k rangements.
s = (8 -10,5)2 + (14 - 10,5)2 + (11 - 10,5)2 + (11- 10,5)2 + (11 - 10,5)2 + (8 - 10,5)2= 25,5
| et | 0,16 |
Exemple
| Variable | a | b | c | d | e | f | g | h | i | j |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 1 | 4,5 | 2 | 4,5 | 3 | 7,5 | 6 | 9 | 7,5 | 10 |
| Y | 2,5 | 1 | 2,5 | 4,5 | 4,5 | 8 | 9 | 6,5 | 10 | 6,5 |
| Z | 2 | 1 | 4,5 | 4,5 | 4,5 | 4,5 | 8 | 8 | 8 | 10 |
| Rj | 5,5 | 6,5 | 9 | 13,5 | 12 | 20 | 23 | 23,5 | 25,5 | 26,5 |
La moyenne des Rj est 16,5.
s = (5,5 - 16,5)2 + (6,5 - 16,5)2 + (9 - 16,5)2 + (13,5 - 16,5)2 + (12 - 16,5)2 + (20 - 16,5)2 + (23 - 16,5)2 + (23,5 - 16,5)2+ (25,5 - 16,5)2 + (26,5 - 16,5)2= 591
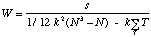 | (E) |
| oﺣﺗ | correspond ﺣ la somme des valeurs de T pour l’ensemble des ex-ﺣ۵quo |
| et |
| et |
|
| pour le rangement de X : |
| = 1 |
| pour le rangement de Y : |
| = 1,5 |
| pour le rangement de Z : |
| = 7 |
et la somme des T = 1 + 1,5 + 7 = 9,5
En utilisant la formule E, nous calculons W corrigﺣ۸ pour les ex-ﺣ۵quo
= 0,828 |
Test de signification de W
Petits ﺣ۸chantillons
Grands ﺣ۸chantillons
ou = k (N -1) W (F) |
Exemple
Nous calculons le ![]() = k (N -1) W = 13 (20 -1) (0,577) = 142,5
= k (N -1) W = 13 (20 -1) (0,577) = 142,5
avec ddl = N - 1 = 20 - 1 = 19
La probabilitﺣ۸ d'obtenir un tel ![]() est p < 0,001. Nous pouvons conclure que l'accord entre les 13 soignants n'est pas alﺣ۸atoire.
est p < 0,001. Nous pouvons conclure que l'accord entre les 13 soignants n'est pas alﺣ۸atoire.