4.2. Cas de deux échantillons indépendants
Bien que l'utilisation de deux échantillons non indépendants soit préférable, cette méthode est fréquemment impraticable. En effet, la nature de la variable étudiée exclue l'utilisation des sujets comme leur propre contrôle. C'est le cas, par exemple, lorsque la variable dépendante est la durée de résolution d'un problème inconnu particulier. Par ailleurs, la réalisation d'échantillons appariés est, nous l'avons vu, délicate. Aussi devons nous utiliser des échantillons indépendants. Ces deux échantillons peuvent être obtenus par deux méthodes : ils sont extraits au hasard dans deux populations ou ils proviennent de l'assignation au hasard de deux traitements aux membres d'un échantillon dont les origines sont arbitraires. Dans tous les cas, les deux échantillons ne doivent pas avoir nécessairement la même taille.
Il est possible d'extraire deux échantillons de militants de deux partis politiques en tirant tous les dizièmes d'une liste alphabétique. Le nombre des membres d'un parti peut ne pas être nécessairement égal à celui des membres de l'autre parti.
Pour tester l'efficacité de l'enseignement de deux professeurs pour une même matière, la moitié des étudiants d'une classe est affectée au hasard à l'un ou à l'autre des enseignants.
4.2.1. Test du Khi carré pour deux échantillons indépendants
Chaque fois que les données sont des fréquences de catégories discrètes, le chi carré peut être mis en oeuvre pour déterminer la signification de différences entre deux groupes indépendants. Les mesures peuvent être nominales.
L'hypothèse testée est généralement que les deux groupes diffèrent par la fréquence relative qui caractérise les membres se répartissant dans les différentes catégories.
Pour cela, nous comptons le nombre de cas de chaque groupe qui appartient aux diverses catégories , et nous comparons la proportion des cas d'un groupe dans les différentes catégories avec la proportion des cas de l'autre groupe.
Méthode
L'hypothèse nulle peut être testée par
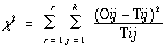 | (7) |
où
Oij = nombre de cas classé dans les i
rangées et les j colonnes.
Tij = nombre de cas attendus classés dans les i
rangées et les j colonnes.
la somme de toutes les cellules des r rangées et des k
colonnes. Le degré de liberté est de (r-1) (k
-1).
Exemple
Pour illustrer la méthode , utilisons des données fictives. Supposons que l'on veuille tester si la taille des individus diffère selon leur qualité de commandement :
43 personnes de petite taille et 52 de grande taille sont classées comme "chef", "éxécutant" ou "inclassable". Les fréquences sont les suivantes :
| Petits | Grands | Total
|
|---|
| Chef | 12 | 32 | 44
|
|---|
| Exécutant | 22 | 14 | 36
|
|---|
| Inclassable | 9 | 6 | 15
|
|---|
| Total | 43 | 52 | 95 = N |
|---|
L'hypothèse nulle implique que la taille des individus est indépendante de leur rangement selon les qualités de classement. La proportion de grands qui sont chefs est la même que celle des petits, ..... Nous pouvons donc déterminer la fréquence attendue dans chaque cellule. Dans chaque cas, nous multiplions les deux totaux marginaux d'une cellule particulière et nous divisons ce produit par N pour obtenir la fréquence
théorique. Ainsi, la fréquence de la cellule supérieure de l'extrême droite de la table est :
E(32) = ((52) (44)) / 95 = 24,08
Dans le tableau suivant, les fréquences théoriques apparaissent en italiques :
| Petits | Grands | Total
|
|---|
| Chef | 19,9
12 | 24,1
32 | 44
|
|---|
| Exécutant | 16,3
22 | 19,7
14 | 36
|
|---|
| Inclassable | 6,8
9 | 8,2
6 | 15
|
|---|
| Total | 43 | 52 | 95 |
|---|
Si les fréquences observées sont voisines des fréquences attendues, leurs différences seront faibles et le c2 sera petit. Lorsque la valeur du c2 est faible nous ne pouvons pas rejeter H0. Au contraire plus cette valeur est élevée, plus les deux groupes ont des chances de différer entre eux.
Les probabilités associées aux différentes valeurs du khi carré sont donnés dans la table 2. Si une valeur observée du c2 est égale ou supérieure à celle donnée dans la table 2 pour un niveau de signification et un degré de liberté, alors nous pouvons rejeter H0 à ce niveau de signification.
Dans notre exemple, le degré de liberté est de (r - 1) (k - 1) = 2 et le calcul du c2 est le suivant :
c2
| 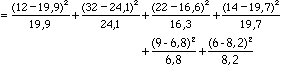 |
c2= 3,14 + 2,59 + 1,99 + 1,65 + 0,71 + 0,59 = 10, 67
La table 2 montre que cette valeur du a est significative au seuil 0,01.
Tables de contingences 2 X 2
Un des cas les plus fréquents d'utilisation du c2 se présente quand les fréquences observées se répartissent en un tableau de contingence 2 x 2. Quand le c2 s'applique à des données dont le r et le k sont égal à 2, la formule suivante peut être mise en oeuvre :
c2
| 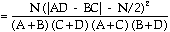 | ddl = 1
| (8)
|
Exemple
Etude de la relation existant entre les intérêts des étudiants brillants, déterminés par test, et leur choix de carrière sur le retrait ou non de l'université. On compare alors les étudiants qui font un choix de carrière en accord avec leurs intérêts déterminés par le test (changement "positif") et les étudiants dont le choix est contraire à leurs intérêts mis en évidence par le test. On pose par hypothèse que les derniers
ont une probabilité élevée de quitter l'université.
H0 il n'y a pas de différence entre les deux groupes. H1 : une proportion supérieure des étudiants, qui font un choix conforme aux résultats de leur test d'intérêt, reste à l'université.
Soit a = 0,05 et N = le nombre d'étudiants pris en compte 80. Comme l'hypothèse alternative prédit la direction de la différence, les test est unilatéral. La table 2 donne les valeurs critiques du c2 pour un test bilatéral.
Le classement des étudiants est le suivant :
| Direction du changement | Total
|
|---|
| Positive | Négative |
|
|---|
| Retrait | A 10 | B 11 | 21
|
|---|
| Reste | C 46 | D 13 | 59
|
|---|
| Total | 56 | 24 | 80 = N |
|---|
Donc, sur les 56 étudiants qui ont fait un choix conforme au résultat de leur test, 10 ont quitté l'université, 46 ont poursuivi leurs études.
La formule (8) nous permet de calculer le c2 de ces données.
c2
| 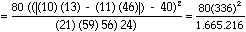 |
c2 = 5,42
La probabilité d'obtenir un tel khi carré dans des conditions d'unilatéralité et avec ddl = 1 est donnée par la table 2 : p < 1/2 (0,02) = 0, 01 < a = 0,05. Nous pouvons rejeter H0. Les étudiants qui font des choix de carrière conformes aux résultats de leur test d'intérêt restent plus fréquemment à l'université que les autres.
Contraintes d'utilisation
Les fréquences théoriques dans chaque cas ne doivent pas être trop faibles.
Tables de contingence 2 x 2 :
- Si N > 40, utiliser la formule (8) ).
- Si N est compris entre 20 et 40, la formule (8) ne peut être utilisé que si toutes les fréquences attendues sont supérieures ou égales à 5. Dans le cas contraire, il est possible d'utiliser un test d'égalité de deux proportions ou test de Fisher.
- Si N < 20, utiliser le test de Fisher.
Tables de contingence à degré de liberté > 1 :
- Moins de 20% des fréquences attendues doivent être inférieures à 5 et aucune inférieure
à 1. Dans le cas contraire, recombiner les catégories en les regroupant seulement si cela ne modifie pas le sens des données.
4.2.2. Test des médianes (Mood test)
C'est un test analogue aux tests d'égalité des moyennes pour des échantillons indépendants. Il a pour principe de déterminer la médiane de l'ensemble des observations et de dénombrer pour chacun des deux échantillons les observations inférieures et les observations supérieures à cette médiane. On obtient ainsi un tableau de contingence 2 x2, à partir duquel on peut effectuer soit un test c2, lorsque les fréquences sont suffisamment élevées, soit un test d'égalité des deux proportions (Fisher).
Les observations initiales sont donc subdivisées en deux catégories par rapport à la médiane générale.
Exemple
Dans deux types de forêts distincts, on a mesuré les hauteurs respectivement de 13 et 14 peuplement choisis au hasard et indépendamment, dans le but de vérifier si les hauteurs médianes des deux types de forêts sont ou ne sont pas égales. a = 0,01.
| Forêt 1 | Forêt 2
|
|---|
| 23,4 | 22,5 | médiane générale = 26,2
N= N1 + N2 = 13 + 14 = 27
|
|---|
| 24,4 | 22,9
|
|---|
| 24,6 | 23,7
|
|---|
| 24,9 | 24,0
|
|---|
| 25,0 | 24,4
|
|---|
| 26,2 | 24,5
|
|---|
| 26,3 | 25,3
|
|---|
| 26,8 | 26,0
|
|---|
| 26,8 | 26,2
|
|---|
| 26,9 | 26,4
|
|---|
| 27,0 | 26,7
|
|---|
| 27,6 | 26,9
|
|---|
| 27,7 | 27,4
|
|---|
| 28,5
|
|---|
Les nombres d'observations inférieures et supérieures ou égales à la médiane générale sont donnés dans le tableau suivant :
| Forêt 1 | Forêts 2 | Total
|
|---|
| x < 26,2 | A 5 | B 8 | 13
|
|---|
| x = or > 26,2 | C 8 | D 6 | 14
|
|---|
| Total | 13 | 14 | 27 = N |
|---|
Quelques observations sont ici égales à la médiane, nous les avons regroupées avec les valeurs supérieures à la médiane. Souvent, elles sont écartées de l'analyse.
Comme N1 = N2 est compris entre 20 et 40 et qu'aucune des fréquences théoriques n'est inférieure à 5, il est possible de calculer le c2 selon la formule (8) .
| c2 | 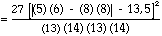 | = 0,34 |
La probabilité d'obtenir un tel c2 pour 1 degré de liberté et un test bilatéral (table 2) est comprise entre 0,70 et 0,50. Elle est supérieure au seuil choisi et nous acceptons l'hypothèse d'identité des deux distributions.
4.2.3. Test des rangs appliqué au cas des échantillons indépendants (Mann-Whitney U test)
La réalisation de ce test est basée sur le classement de l'ensemble des observations par ordre croissant, la détermination du rang de chacune d'elles, et le calcul de la somme des rangs relative à l'échantillon qui comporte le plus petit nombre d'observations.
Soit n1 le nombre d'observations du plus petit échantillon et n2 le nombre d'observations du plus grand échantillon. Les observations des deux échantillons sont rangées en ordre croissant. Dans ce cas, le rangement prend en compte les valeurs algébriques, c'est-à-dire que le rang le plus faible est assigné à l'observation dont la valeur est la plus négative. On recherche alors la valeur statistique U du test qui est
donné par le nombre de fois qu'un score du groupe n2 précède un score du groupe n1 lors du rangement.
Ainsi si l'on dispose d'un groupe expérimental de 3 cas (n1) et d'un groupe contrôle de 4 cas (n2) et que les observations sont les suivantes :
| Observations E | 9 | 11 | 15 |
|
|---|
| Observations C | 6 | 8 | 10 | 13 |
|---|
Nous rangeons les observations en ordre croissant en conservant l'identité de chacune d'entre-elles.
| 6 | 8 | 9 | 10 | 11 | 13 | 15
|
|---|
| C | C | E | C | E | C | E |
|---|
Maintenant considérons le groupe E et calculons le nombre d'observations C qui précède chacune de celle du groupe E. Pour l'observation 9 de E, deux observations de C précèdent ; pour l'observation 11 de E, trois C précèdent ; pour l'observation 15 de E, quatre C précèdent.
Donc U = 2 + 3 + 4 = 9.
Le principe du test consiste à rejeter l'hypothèse d'identité des deux distributions lorsque la valeur observée U, s'écarte trop de la valeur attendue correspondante. Pour des échantillons très petits (3 < n2 < 8), on dispose de tables qui donnent la probabilité exacte d'obtenir tout U aussi extrême que celui observé (Tables 6). Il suffit alors de connaître n1 (la taille du plus petit échantillon), n2 et U
et de se reporter à la table 6 pour la valeur de l'échantillon n2. Les probabilités données dans ces tables sont
unilatérales. Pour un test bilatéral, il faut doubler la valeur de la table.
Dans notre exemple : n1 =3, n2 = 4, U = 9, nous consultons la table 6 pour n2 = 4, mais la valeur observée de U n'apparaît pas dans la table. Par contre, si nous avions calculé le nombre d'observations E qui précèdent celle du groupe C, le U obtenu serait égal à 0 + 0 + 1 + 2 = 3. Cette valeur se trouve dans la table. Il est toujours possible de rechercher le plus petit U observé par la formule
U = n1n2 - U' (9)
La probabilité unilatérale d'obtenir un U 3 est p
= 0,200.
Lorsque la taille de n1 et n2 augmentent la méthode de comptage décrite devient rapidement inutilisable et une méthode alternative rend ce calcul plus aisé.
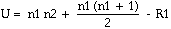 | (10) |
ou de façon équivalente
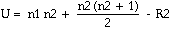 | (11) |
où R1 = somme des rangs assignés à l'échantillon le plus petit (n1)
et R2 = somme des rangs assignés à l'autre échantillon.
Exemple pour un petit échantillon
- Cinq rats sont entraînés à imiter un rat leader dans un labyrinthe en T, pour atteindre une source de nourriture. Puis ces rats sont ensuite transférés dans une situation où par imitation d'un rat leader, ils apprennent à éviter un choc électrique. Leur comportement dans cette situation est comparé à celui de rats n'ayant pas été entraînés à suivre un leader. La comparaison se fait en terme de nombre d'essais nécessaire à chaque rat pour obtenir 10 réponses d'évitement lors de 10 essais. On fait l'hypothèse que les 5 rats préalablement conditionné à imiter un congénère réussiront plus rapidement que les autres à éviter les chocs.
Soit a = 0,05 ; n1 = 4 rats témoins et n2 = 5 rats expérimentaux. Les
résultats sont les suivants :
| Exp | Rang | Témoins | Rang
|
|---|
| 78 | 7 | 110 | 9
|
|---|
| 64 | 4 | 70 | 5
|
|---|
| 75 | 6 | 53 | 3
|
| 45 | 1 | 51 | 2
|
|---|
| 82 | 8
| |
|
| R2 = 26 | | R1 = 19 |
donc en appliquant la formule (11),
nous avons
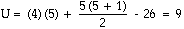
La probabilité d'obtenir un U 9 dans ces conditions est p
= 0,452 (Table 6, n2 = 5).
Les données ne supportent pas l'hypothèse selon laquelle un entraînement à l'imitation préalable est généralisé à d'autres situations.
Echantillons dont n2 est compris entre 9 et 20
Les tables 6 ne sont plus utilisables lorsque n2 devient supérieur à 8. Mais on peut alors faire usage des tables 7 pour les échantillons n2 dont la taille est comprise entre 9 et 20 et n1 20. Ces tables 7 donnent les valeurs critiques de U à différents niveaux de signification. Ainsi, lorsque la valeur du U observé est inférieur ou égale à celle de la table, H0 peut
être rejeté au niveau de signification correspondant.
Grands échantillons (n2 > à 20)
Quand la taille de n1 et de n2 augmente, la distribution de U s'approche de la distribution normale. L'approximation normale se calcule de la façon suivante :
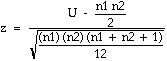 | (12) |
Dans des sociétés humaines à culture non écrite, les ethnologues peuvent classer ces sociétés en fonction du degré d'anxiété présenté par les enfants à la suite de la
socialisation (ce classement va de 6 à 17). Il est aussi possible de distinguer deux
groupes suivant que ces sociétés disposent d'explications orales de la maladie ou non.
| Explication absente | Estimation anxiété | Rang | Explication présente | Estimation anxiété | Rang
|
|---|
| Lapp | 13 | 29,5 | Marquesan | 17 | 39
|
|---|
| Chamorro | 12 | 24,5 | Dobuan | 16 | 38
|
|---|
| Samoan | 12 | 24,5 | Baiga | 15 | 36
|
|---|
| Arapesh | 10 | 16 | Kwoma | 15 | 36
|
|---|
| Balinese | 10 | 16 | Thonga | 15 | 36
|
|---|
| Hopi | 10 | 16 | Alorese | 14 | 33
|
|---|
| Tanala | 10 | 16 | Chagga | 14 | 33
|
|---|
| Paiute | 9 | 12 | Navaho | 14 | 33
|
|---|
| Chenchu | 8 | 9,5 | Dahomean | 13 | 29,5
|
|---|
| Teton | 8 | 9,5 | Lesu | 13 | 29,5
|
|---|
| Flathead | 7 | 5 | Masai | 13 | 29,5
|
|---|
| Papago | 7 | 5 | Lepcha | 12 | 24,5
|
|---|
| Venda | 7 | 5 | Maori | 12 | 23,5
|
|---|
| Warrau | 7 | 5 | Pukapukan | 12 | 24,5
|
|---|
| Wogeo | 7 | 5 | Trobriander | 12 | 24,5
|
|---|
| Ontong-Javanese | 6 | 1,5 | Kwakiutl | 11 | 20,5
|
|---|
| | R1 = 200,0 | Manus | 11 | 20,5
|
|---|
| | | Chiricahua | 10 | 16
|
|---|
| | | Comanche | 10 | 16
|
|---|
| | | Siriono | 10 | 16
|
|---|
| | | Bena | 8 | 9,5
|
|---|
| | | Slave | 8 | 9,5
|
|---|
| | | Kurtachi | 6 | 1,5
|
|---|
| | | | | R2 = 580,0 |
|---|
Noter que les valeurs d'anxiété qui sont ex-aequo, où qu'elles se présentent, sont affectées d'un rang égal à la moyenne des rangs revenant normalement à ces différentes
valeurs.
Nous calculons la valeur de U par la formule (10).
Nous substituons la valeur de U dans la formule 12 pour cacluler .
z = = 3, 43
La référence à la table 1
révèle que zégal ou supérieur à 3,43 a une probabilité unilatérale de p < 0,0003. Comme ce p est inférieur à a = 0,01, nous pouvons rejeter H0. Nous concluons que les sociétés à explications orales de la maladie ont une socialisation de l'anxiété supérieure aux autres sociétés.
Problème des ex-aequo
Lorsque deux ou plus d'observations du même groupe ont des valeurs égales, la valeur de U n'est pas affectée. Par contre, si des valeurs identiques se présentent dans les deux échantillons, la valeur du U est affectée. Bien que cet effet soit souvent négligeable, une correction pour les ex-aequo existe. La formule corrigée pour les ex-aequo est la suivante :
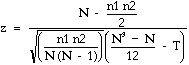 | (13)
|
| où N = n1 = n2 et | 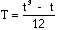 | ; t est le nombre d'ex-aequo pour un rang donné. |
Pour les données précédentes n1 + n2 = 16 + 23 = 39 = N, nous observons les ex-aequo suivants :
2 pour 6 ; 5 pour 7 ; 4 pour 8 ; 7 pour 10 ; 2 pour 11 ; 6 pour 12 ; 4 pour 13 ; 3 pour 14 ;
3 pour 15.
T = 0,5 + 10,0 + 5,0 + 28,0 + 0,5 + 17,5 + 5,0 + 2,0 + 2,0 = 70,5
L'utilisation de ces valeurs dans la formule (13)
donne :
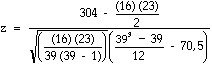 | = 3, 45
|
Cet exemple confirme que les ex-aequo ont un effet négligeable sur la valeur du z. Aussi la corection peut n'être faite que lorsque le nombre d'ex-aequo est très important où lorsque la valeur du z obtenue sans correction est voisine de la signification au seuil choisi.
4.2.4. Test de Kolmogorov-Smirnov pour deux échantillons (Kolmogorov-Smirnov two sample test)
Il permet de tester si deux échantillons indépendants sont extrait de la même population ou de populations ayant la même distribution.
Le test bilatéral est sensible à toute différence entre les distributions d'où ont été extrait les échantillons. Le test unilatéral permet de prédire si les observations d'un groupe expérimental sont "meilleures" que celles du groupe contrôle.
Il compare deux distributions cumulatives et est concerné par la concordance entre deux séries de valeurs. Il recherche la plus grande déviation existant entre les deux distributions cumulatives.
Méthode
Il faut réaliser la distribution cumulative de fréquence pour chaque échantillon, avec les mêmes intervalles pour les deux distributions. Pour chaque intervalle nous calculons la différence entre les deux distributions et nous recherchons la plus forte de ces déviations.
- D = maximum
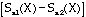 pour un test unilatréral (14)
pour un test unilatréral (14)
ou
- D = maximum
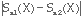 pour un test bilatéral (15)
pour un test bilatéral (15)
Il faut noter que dans un test unilatéral nous trouvons la valeur maximum de D dans la direction prédite (formule 14),alors que pour un test bilatéral nous trouvons la valeur maximum absolue de D (formule 15).
Lorsque l'on utilise des données pour lesquelles la taille et le nombre d'intervalles est arbitraire, il est préférable d'utiliser le plus d'intervalles possibles, de façon à perdre le moins d'information possible.
Petits échantillons
Quand n1 = n2 = N et quand ensemble ils sont inférieurs ou égaux à 40, la table 8 donne les valeurs critiques de KD, qui est le numérateur de la plus large différence observée entre les deux distributions cumulatives, c'est-à-dire le numérateur de D.
Quand n1 = n2 = N et quand ensemble ils sont inférieurs ou égaux à 20, la table 8a donne les valeurs critiques de D.
Quand n1 = n2 sont différents et égaux ou inférieurs ‡ 20, la table 8b donne les valeurs critiques de D pour un test bilatéral. Alors que la table 8c donne les valeurs critiques de D pour un test unilatéral.
Exemple
On compare des séries de matériel appris par des collégiens de 6ème et de 4ème. On veut tester l'effet de prééminence, tendance à se souvenir de façon plus efficace du matériel appris précocément dans une série que du matériel appris en dernier. On compare alors le pourcentage d'erreurs commises par deux groupes sur la première moitié des choses apprises dans une série, en prédisant que les enfants les plus âgés feront moins d'erreurs en répétant ces choses que les enfants plus jeunes. L'effet de prééminence est moins marqué chez les jeunes enfants.
Soit 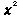 = 0,01; n1 = n2 = N, nombre de sujets dans chaque groupe = 10 et comme H1
prédit la direction de la différence, les test est unilatéral. Les pourcentages d'erreurs commises par chaque sujet lors du rappel des notions apprises lors de la première moitié d'une série sont :
= 0,01; n1 = n2 = N, nombre de sujets dans chaque groupe = 10 et comme H1
prédit la direction de la différence, les test est unilatéral. Les pourcentages d'erreurs commises par chaque sujet lors du rappel des notions apprises lors de la première moitié d'une série sont :
| 6ème | 4ème
|
|---|
| 39,1 | 35,2
|
|---|
| 41,2 | 39,2
|
|---|
| 45,2 | 40,9
|
|---|
| 46,2 | 38,1
|
|---|
| 48,7 | 29,1
|
|---|
| 48,4 | 34,4
|
|---|
| 40,6 | 24,3
|
|---|
| 52,1 | 32,4
|
|---|
| 47,2 | 32,6
|
|---|
| 55,0 | 41,8 |
|---|
On réalise à partir de ces données, deux distributions de fréquences cumulatives.
| % d'erreurs total dans la 1ère moitié de la série
|
|---|
| 24-27 | 28-31 | 32-35 | 36-39 | 40-43 | 44-47 | 48-51 | 52-55
|
|---|
| S101 (X) | 1/10 | 2/10 | 5/10 | 7/10 | 10/10 | 10/10 | 10/10 | 10/10
|
|---|
| S102 (X) | 0/10 | 0/10 | 0/10 | 0/10 | 3/10 | 5/10 | 8/10 | 10/10
|
|---|
| Sn1 (X) - Sn2 (X) | 1/10 | 2/10 | 5/10 | 7/10 | 7/10 | 5/10 | 2/10 | 0 |
|---|
La plus grande différence observée entre les deux séries est 7/10. Donc KD = 7, la table 8 révèle que quand N = 10, une valeur de KD = 7 est significative au seuil a = 0,01 pour un test unilatéral. Nous rejetons H0 et concluons que les élèves de 4ème font proportionnellement moins d'erreurs que les 6ème lors du rappel du matériel de la première moitié apprise de séries.
Grands échantillons : test bilatéral
Lorsque n1 et n2 sont supérieur à 40, il est possible d'utiliser la table 9. Dans ce cas, n1 et n2 ne doivent pas nécessairement être égaux. Pour déterminer D, on utilise la formule 15. Puis comparer la valeur observée à la valeur critique obtenue en substituant les valeurs n1 et n2 dans l'expression donnée dans la table 9. si la valeur observée de D est égale ou supérieure à celle calculée à partir de
l'expression de la table, H0 peut être rejeté au niveau de signification associée à l'expression.
Soit n1 = 55 et n2 = 60, a = 0,05 . La valeur de D devra être supérieure ou égale à la valeur calculée à partir de la table 9 pour rejeter H0, soit
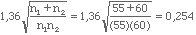
Grands échantillons : test unilatéral
Lorsque n1 et n2 sont grands, on calcule D par la formule (14) . Dans ce cas, l'hypothèse alternative pose que les valeurs de la population dont a été extrait l'un des échantillons sont plus élevées que celles de la population
dont est extrait le deuxième échantillon.
Il a été montré que :
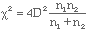 | (16)
|
a une distribution qui s'approche de celle du chi carré à deux degré de liberté. En substituant la valeur observée de D dans la formule 16 et en se reportant à la table de la dsitribution du chi carré (table 2), il est possible de déterminer la signification de la valeur observée de D.
Discussion
Les tests présentés sont plus ou moins sensibles à différentes sortes de différences entre les échantillons. Si l'on veut les différences concernant la tendance centrale entre deux populations dont sont extrait les deux échantillons, il faut choisir le test des médianes, les test de Mann-whitney ou le test de Kolmogorov-Smirnov. Par contre, si l'on veut déterminer si deux échantillons appartiennent à des populations qui diffèrent à tout point de vue : tendance centrale ou dispersion ou aplatissement...., il faut choisir le test du chi carré, le test de Kolmogorv-smirnov bilatéral.






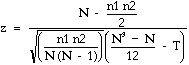
![]() pour un test unilatréral (14)
pour un test unilatréral (14)
![]() pour un test bilatéral (15)
pour un test bilatéral (15) = 0,01; n1 = n2 = N, nombre de sujets dans chaque groupe = 10 et comme H1
prédit la direction de la différence, les test est unilatéral. Les pourcentages d'erreurs commises par chaque sujet lors du rappel des notions apprises lors de la première moitié d'une série sont :
![]()
![]()